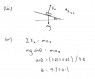Vector diagrams and Calculating Angles

[FollowTheFez]

Homework Statement

A cart of mass 357g is sent traveling down a frictionless sloped track.
It's acceleration is 1.65ms^-2.
1. Draw a labelled free body diagram of the cart while it is accelerating down the track.
2. Using Newton's second law, calculate the slope of the track.

Homework Equations

SOH CAH TOA

F=ma

The Attempt at a Solution

I've got the model answers and I got the correct free body diagram (see attached).
What I don't understand is that when they change the x,y axis, where does θ end up?


Same diagram as attached, but I tried calculating like this without changing the axis...

F due to gravity = mg
F = 3.57kg x 9.8
F = 34.986N

Which would be the vertical component.

Hypotenuse would just be the acceleration at and angle down the slope.
F=ma
F = 3.57kg x 1.65
F = 5.8905N

Then by looking at SOH CAH TOA (I do need these to see why sin or cos is used!), we have the components opposite to the angle and the hypotenuse. Therefore we use sin.

sinθ = $\frac{Opposite}{Hypotenuse}$
θ = sin^-1 $\frac{Opposite}{Hypotenuse}$
θ = sin^-1 $\frac{34.986}{5.8905}$
θ = MATH ERROR $\leftarrow$ That's what appears on my calculator when I plug it all in.

Can someone please tell me what I'm doing wrong? Can I calculate the answer without altering the axis? And if altering the axis would make it easier, where does θ end up?
I don't understand how the model answer has been worked.

 

[462chevelle]

is that the correct usage of inverse sin? I ask because I don't know myself.

 

[FollowTheFez]

is that the correct usage of inverse sin? I ask because I don't know myself.

If moving cos, sin or tan from one side of an equation to the over you must always take the inverse of it, if that's what you mean. I think I get "Math Error" because my opposite value is larger than my hypotenuse value. Which seems illogical. However I don't see any other value each of these could be.

 

[462chevelle]

http://library.thinkquest.org/10796/ch1/ch1.htm
go to chapter 5 here. I am trying to look and see if I can figure it out but the equation or method should be in that chapter.

 

[462chevelle]

shouldn't be solving for theta. should be using tangent right? it wants the slope

 

[462chevelle]

the only error I can find up to this point is where the decimal is. guess your going to have to wait for someone smarter lol.

 

[SteamKing]

How many grams are in 1 kg?

 

[462chevelle]

1000. so It would be .357

 

[invertioN]

Poster above is correct, your first calculation is wrong. 357 grams is 0.357 kg, so your force is mg=3.4986 N

 

[462chevelle]

I think we need to turn the vector where the hypotenuse is the greatest force. I am at work right now and can't try to solve it but I think that's how to do it.

 

[Tyrannosaurus_]

Hi,

The triangle you made is impossible, & that's why you get the error. It's not possible for the hypotenuse to be less than the sum of the other two sides.

As for your question about where the angle of the ramp goes, consider the following images.

Image 1. Box on a ramp with angle of incline shows the angle
Image 2. Box on a ramp with a FBD.

Notice that the angle of incline for the ramp, is the same angle that you find when you divide the force of gravity into the component of gravity down the track, and the component of gravity perpendicular to the track.

Does that help you see the angles, and why sinθ produces the component of gravity down the track?

(Obviously, there must not be any friction for your FBD to be true.)