Vector Projection Homework: Figuring Out the Angle

  • Thread starter Thread starter iflabs
  • Start date Start date
  • Tags Tags
    Projection Vector
AI Thread Summary
To project vector A onto the x and y axes, determine the angle it makes with line C, which is parallel to the x-axis. Since vector A is perpendicular to vector B and forms a right triangle with line C, the angle A makes with C is the complement of 30 degrees, resulting in a 60-degree angle. This angle is also the same when extended to the x-axis due to corresponding angles in parallel lines. Therefore, the angle used for the projection of vector A onto the axes is 60 degrees. Understanding these relationships is crucial for accurately performing vector projections.
iflabs
Messages
11
Reaction score
0

Homework Statement



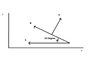
I have a vector diagram attached below. Vector A is perpendicular to vector B.

How do you figure out what angle to use in order to project vector A onto the x and y axis?


Homework Equations



A dot B = ABcos(angle)

The Attempt at a Solution



180-30-90 = 60?
 

Attachments

  • vectors.jpg
    vectors.jpg
    9.9 KB · Views: 477
Physics news on Phys.org
Exactly right- though you don't really need the "180" and "90". Extend A back to line C and you will see that the three lines form a right triangle. That tells you that the angle A makes with C is the complement of 30 degeres, 60. And, since C is parallel with the x-axis, extending it further shows (corresponding angles in parallel lines) that it makes the same angle with the x-axis.
 

Thread 'Family of lines that are at a distance of 5 from the origin'

I picked up this problem from the Schaum's series book titled "College Mathematics" by Ayres/Schmidt. It is a solved problem in the book. But what surprised me was that the solution to this problem was given in one line without any explanation. I could, therefore, not understand how the given one-line solution was reached. The one-line solution in the book says: The equation is ##x \cos{\omega} +y \sin{\omega} - 5 = 0##, ##\omega## being the parameter. From my side, the only thing I could...
View full post »

Similar threads

What Is the Correct Angle Between Vectors a and c?
Replies
4
Views
2K
How Do I Calculate the Angle Between Vectors in Vector Projection Problems?
Replies
7
Views
2K
Finding the angle between vectors a and m, knowing the magnitude of m and n
Replies
2
Views
2K
To find the component of a vector perpendicular to another
Replies
20
Views
3K
Vector dot product and parallel vectors
Replies
6
Views
4K
Is the Sine Rule Valid for Non-Triangular Vector Configurations?
Replies
3
Views
2K
Vectors: Proving the value of a•(b x c)
Replies
21
Views
8K
Proving that ABE is a Straight Line: Vector Method
Replies
11
Views
5K
I need to figure this out: (A×B)⋅C
Replies
6
Views
9K
Projecting a Vector onto a Plane
Replies
4
Views
3K

Hot Threads

Recent Insights

Back
Top