Vectors and points on a circle

[Saitama]

Homework Statement

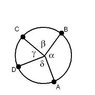
Let A, B, C, D be distinct points on a circle with centre O. If there exists non zero real numbers x and y such that $|x\vec{OA}+y\vec{OB}|=|x\vec{OB}+y\vec{OC}|=|x\vec{OC}+y\vec{OD}|=|x \vec{OD}+y\vec{OA}|$, then which of the following is always true?
A)ABCD is a trapezium
B)ABCD is a rectangle
C)ABCD is a rhombus
D)ABCD is a square

Homework Equations

The Attempt at a Solution

Honestly, I have no idea how to begin with this problem. Should I start by squaring the moduli? I don't know if that would help.

Any help is appreciated. Thanks!

 

[Saitama]

Anyone?

 

[ehild]

Pranav, which statement is certainly true? ehild

 

[Saitama]

Pranav, which statement is certainly true?


ehild

If I start by assuming x=y=1, it comes out that its a square. But how would I prove it for a general case?

 

[haruspex]

I find it easiest to approach this geometrically.
All that matters wrt x and y is the ratio. If yOA, yOB, yOC, yOD lie on a circle radius y around O, where do xOA etc. lie? Now, cheating a bit, let's take x as negative and look at the locations of |x|OA etc., so xOA+yOA = yOA-|x|OA, allowing us to look at the line joining the two points instead of a vector sum. Look at the triangle formed. What formula can you think of for |yOA-(|x|)OA|?

 

[haruspex]

I find it easiest to approach this geometrically.
All that matters wrt x and y is the ratio. If yOA, yOB, yOC, yOD lie on a circle radius y around O, where do xOA etc. lie? Now, cheating a bit, let's take x as negative and look at the locations of |x|OA etc., so xOA+yOA = yOA-|x|OA, allowing us to look at the line joining the two points instead of a vector sum. Look at the triangle formed. What formula can you think of for |yOA-(|x|)OA|?

 

[ehild]

The magnitude of all vectors OA,OB,OC,OD are 1. Let the angles between two of them α,β,γ,δ.
Find the magnitude of xOA+yOB, ... in terms of x,y,and the corresponding angles applying the law of cosines.

ehild

 

[Saitama]

Sorry for the late reply.

The magnitude of all vectors OA,OB,OC,OD are 1. Let the angles between two of them α,β,γ,δ.
Find the magnitude of xOA+yOB, ... in terms of x,y,and the corresponding angles applying the law of cosines.

ehild

That's an excellent hint, ehild! Thanks a lot!

It can be done without assuming the radius to be one.
Referring to your attachment,
|x\vec{OA}+y\vec{OB}|=x^2|\vec{OA}|^2+y^2|\vec{OB}|^2+2xy|\vec{OA}|| \vec{OB} |\cos \alpha
Similarly we can obtain expressions for $|x\vec{OB}+y\vec{OC}|$, $|x\vec{OC}+y\vec{OD}|$ and $|x\vec{OD}+y\vec{OA}|$ and using the fact that $|\vec{OA}|=|\vec{OB}|=|\vec{OC}|=|\vec{OD}|$, I get
\cos \alpha=\cos \beta=\cos \gamma=\cos \delta
\Rightarrow \alpha=\beta=\gamma=\delta=\frac{\pi}{2}

This proves that these points form a square.

Thanks ehild!

 

[ehild]

You have to work a bit more on it. Two angles are not necessarily the same if their cosines are the same.
And about the questions. Is it not true that ABCD is a rectangle? Or trapezium? Rhombus?

ehild

 

[Saitama]

You have to work a bit more on it. Two angles are not necessarily the same if their cosines are the same.
And about the questions. Is it not true that ABCD is a rectangle? Or trapezium? Rhombus?

ehild

Yes, you are right, I need to work more on it.

It is not rhombus because in a rhombus, the diagonals are not equal. In trapezium too, the diagonals are not equal.

How would I show that it isn't a rectangle?

I am not sure how would I do it but here's my take on it. Assuming that one of the angles between the diagonals is $\alpha$ and its cosine is $\cos \alpha$, the other angle is $\pi-\alpha$ and its cosine $-\cos \alpha$ but this is contrary to the relation of cosines being equal, hence this isn't a rectangle.

Is this correct?

 

[haruspex]

It is not rhombus because in a rhombus, the diagonals are not equal. In trapezium too, the diagonals are not equal.

In my understanding of these terms, every square is also a rhombus and a rectangle and a trapezium. They are not mutually exclusive.

 

[ehild]

In my understanding of these terms, every square is also a rhombus and a rectangle and a trapezium. They are not mutually exclusive.

and a quadrilateral, with a=b, and 90° angle between the diagonals.

ehild

 

[Saitama]

and a quadrilateral, with a=b, and 90° angle between the diagonals.

ehild

Is my proof still incomplete?

 

[haruspex]

Is my proof still incomplete?

I think the issue of cos α = cos β still needs some work. What are the possible solutions of that for each being in the range 0 to 2 pi?

 

[Saitama]

I think the issue of cos α = cos β still needs some work. What are the possible solutions of that for each being in the range 0 to 2 pi?

$\beta=±\alpha$ ?

 

[haruspex]

$\beta=±\alpha$ ?

That wouldn't allow both to be in the range 0 to 2 pi.

 

[Saitama]

That wouldn't allow both to be in the range 0 to 2 pi.

This would be silly but is $\alpha=\pi+\beta$ or $\alpha=\pi-\beta$?

 

[ehild]

Well, if one of the angles is α1=(π-β), the other α2=π+β, and β≠π/2, what could be the other angles with the same cosine?


ehild.

 

[ehild]

$\beta=±\alpha$ ?

Or β=2π-α...


ehild

 

[Saitama]

Or β=2π-α...


ehild

Thanks but how should I complete my proof now?

 

[ehild]

Assume that not all angles are equal, but α1=β and α2=2pi-β. What possibility would you have for the other two angles?


ehild