kariibex
- 9
- 0
Homework Statement
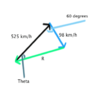
A plane is steering N45°E with an airspeed of 525 km/h. The wind is from N60°W at 98 km/h. Find the ground speed and the direction of the plane.
Homework Equations
Cosine law, sine law, vector addition/subtraction.
The Attempt at a Solution
I have attached an image of my diagram (sorry for the messiness!)
I Solved for R using the cosine law:
R^2 = 525^2 + 98^2 - 2(525)(98)cos60°
R^2 = 285229 - 102900cos60
R^2 = 233779
R = 483.5 km/h
As for the angle, theta, I also used the cosine law:
98^2 = 525^2 + 483.5^2 = 2(525)(483.5)cosθ
-499793.25 = -507675cosθ
cosθ = 0.9844
θ = 10.1°
Is my method correct?
Thank you in advance!