kenji1992
- 22
- 0
Vectors -- velocity is changing but speed is not...
Which pair of vectors represent an object whose velocity is changing but whose speed is NOT changing?
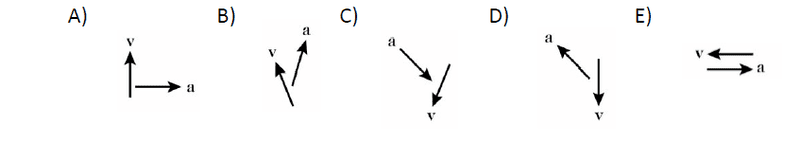
E? V is going left, indicating negative, while acceleration goes in the other direction.
Homework Statement
Which pair of vectors represent an object whose velocity is changing but whose speed is NOT changing?
Homework Equations
The Attempt at a Solution
E? V is going left, indicating negative, while acceleration goes in the other direction.