- #1
cheerspens
- 92
- 0
Homework Statement
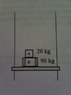
Two blocks are stacked on a platform, which is attached to two cables as shown in the attached figure. If it takes 5.0 sec for the platform to reach a speed of 11.5 m/s directed upward starting from rest find the following information:
After a total of 10 sec of acceleration, the cables suddenly bring the platform to an abrupt stop. Block B is attached to the platform, but block A is free to move. How high above the ground will the block A rise? Not that the platform was initially resting on the ground just before the cables accelerated it upward.
Homework Equations
x=xo+vot+(1/2)at2
v=vo+at
The Attempt at a Solution
I found the acceleration to be 2.3 m/s2.
How should I set this up? I usually start off with a variable list but how do I take into account that block A is going to continue moving?