Velocity & Energy Homework: Find Speed at Low/High Points

[TS656577]

Homework Statement

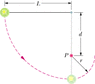
The string in Fig. 8-37 is L = 129 cm long, has a ball attached to one end, and is fixed at its other end. The distance d from the fixed end to a fixed peg at point P is 78 cm. When the initially stationary ball is released with the string horizontal as shown, it will swing along the dashed arc. What is its speed when it reaches (a) its lowest point and (b) its highest point after the string catches on the peg?

Homework Equations

K=1/2mv^2
U=mgh where in this case, h=L

The Attempt at a Solution

I know I need to use the conservation of energy (U(i) + K(i) = U(f) + K(f)) and then K(i)=0 and U(f)=0. So then you can use the equation mgL = 1/2mv^2 and the m's cancel out so youre left with gL = 1/2v^2. I took this to mean that I would have 9.8(129) = 1/2v^2. Solving for v, I got 50.28 m/s. The online program says that's wrong so I'm at a loss.

 

[TS656577]

I'm still at a loss for this one