phoenixXL
- 49
- 4
Homework Statement
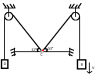
A bead C can move freely on a horizontal rod. The bead is connected by blocks B and D by a string as shown in the figure. If the velocity of B is v. Find the velocity of block D.
Homework Equations
As the string is inextensible the velocity of the string along the length is const.
The Attempt at a Solution
The doubt I have is that, the following should be true
v_c\ =\ v_b.cos53°\ \ \ \ ...(1)
But in the solution from the book I get that
v_b\ =\ v_c.cos53°\ \ \ \ ...(2)
I used relation 1 and got wrong results, I'm just confused how do we get relation 2.
Kindly help me out.
Thanks for your time