Verifying Greens Theorem for Region R with P(x,y)=xy, Q(x,y)=x^2

[smoothman]

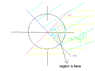
how can greens theorem be verified for the region R defined by (x^2 + y^2 \leq 1), (x + y \geq 0), (x - y \geq 0) ...<br /> P(x,y) = xy, Q(x,y) = x^2

> okay i know \int_C Pdx + Qdy = \int\int \left(\frac{dQ}{dx} - \frac{dp}{dy}\right) dA

so: \int_C xy dx + x^2dy = \int\int_D \left(2x - x\right) dy dx

.........
here's my problem:
the limits of integration for the region D expressed as polar co-ordinates are:
-\frac{\pi}{4}\leq \theta \leq \frac{\pi}{4} \mbox{ and }0\leq r\leq 1

i understand "r" is from 0 to 1 because of the radius...
but how do you explain why theta is from -pi/4 to pi/4
-------------------------------
anyways using those limits for integration this is what i got:

ok so using polar co-ordinates:
2x - x = x
in polar terms: x = rcos\theta

so the integral is now:

\int_C xy dx + x^2dy = \int^{\pi/4}_{-\pi/4}\int^1_0 \left(rcos\theta\right)(r) drd\theta = \int^{\pi/4}_{-\pi/4}\left[\frac{1}{3}r^3cos\theta\right]^1_0d\theta = \int^{\pi/4}_{-\pi/4}\left[\frac{1}{3}cos\theta\right]d\theta = \left[\frac{1}{3}sin\theta\right]^{\pi/4}_{-\pi/4} = \frac{2}{3}sin(\pi/4)<br />

is my result correct?
--------------------------
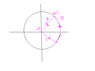
lastly, the curl integral can be shown using three line integrals:
<br /> \bold{r}_1(t) = t\cos \frac{\pi}{4}\bold{i}-t\sin \frac{\pi}{4}\bold{j} \mbox{ for }0\leq t\leq 1<br />
<br /> \bold{r}_2(t) = t\cos \frac{\pi}{4}\bold{i}+t\sin \frac{\pi}{4}\bold{j} \mbox{ for }0\leq t\leq 1<br />
<br /> \bold{r}_3(t) = \cos t\bold{i} + \sin t \bold{j} \mbox{ for }-\frac{\pi}{4} \leq t\leq \frac{\pi}{4}<br />

can you please explain why the line integrals are as they are.

 

[matness]

how do you explain why theta is from -pi/4 to pi/4

First draw the region given to you .
(x^2 + y^2 \leq 1), (x + y \geq 0), (x - y \geq 0)

The boundary of region is determined by the lines x=y, x=-y and the circle x^2+y^2\eq 1
Circle gives you first limit 0\leq r\leq 1
and these two lines gives you limit for theta
(x=y and x=-y makes angle pi/4 w.r.t x-axis)
And by the inequalities you conclude theta should be between -pi/4 and pi/4

 

[matness]

why the line integrals are as they are

They are the curves on which you will evaluate your line integral directly
If you did draw the region correctly
you will see (it is like a slice of a pizza) r1 r2 and r3 are the linesegmentsbounding the region
To be more clear

r1 is part of x-y=0
x=rcos(theta) y=r sin(theta) and you know theta =pi/4 and r changes from 0 to 1 (you can replace r by t anyway just notation)
The others are similiar
r2 is part of x+y=0
r3 is part of the circle which is an arc from -pi/4 to pi/4 with radius 1
edit:region is drawn in the picture

 

[heyo12]

just checking

 

[smoothman]

thanks for this one: from the information provided here is what i managed to work out:

i know \int Pdx + Qdy = \int xy dx + \int x^2 dy since P=xy and Q=x^2

for r1(t)
<br /> \bold{r}_1(t) = t\cos \frac{\pi}{4}\bold{i}-t\sin \frac{\pi}{4}\bold{j} \mbox{ for }0\leq t\leq 1<br />

so:

\int_c xy dx + \int_c x^2 dy= \int^1_0 -\frac{1}{2}t^2(sin\frac{\pi}{2})(cos\frac{\pi}{4}) dt + \int^1_0 t^2(cos^2\frac{\pi}{4})(-sin\frac{\pi}{4}) dt<br />

= \int^1_0 -\frac{1}{2}t^2(cos\frac{\pi}{4}) dt + \int^1_0 -\frac{1}{2}t^2(sin\frac{\pi}{4}) dt<br />

= \left[-\frac{1}{6} t^3 cos(\pi/4) \right]^1_0 + \left[-\frac{1}{6} t^3 sin(\pi/4) \right]^1_0

= -\frac{1}{6}cos(\pi/4) + -\frac{1}{6}sin(\pi/4)

for r2(t)

<br /> \bold{r}_1(t) = t\cos \frac{\pi}{4}\bold{i}-t\sin \frac{\pi}{4}\bold{j} \mbox{ for }0\leq t\leq 1<br />

i got: \frac{1}{6}cos(\pi/4) + \frac{1}{6}sin(\pi/4)SO THE LINE INTEGRALS OF r1(t) and r2(t) cancel each other out.

for r3(t)... This is where I am having problems

<br /> \bold{r}_3(t) = \cos t\bold{i} + \sin t \bold{j} \mbox{ for }-\frac{\pi}{4} \leq t\leq \frac{\pi}{4}<br />

\int_c xy dx + \int_c x^2 dy = \int^\frac{\pi}{4}_\frac{-\pi}{4}-cos(t)sin^2(t) dt<br /> + \int^\frac{\pi}{4}_\frac{-\pi}{4}cos^3(t)<br />

but i can't seem to do any more of it.. stuck here.. how do i complete it
..........
ok the questions:
(a) were my line integrals of r1 and r2 correct
(b) what is the answer of r3
(c) is the final answer of these line integrals \frac{2}{3}sin(\pi/4)<br />

 

[matness]

(c) We have to find \frac{2}{3}sin(\pi/4)
Because using greens theorem you did so.

(b)\int_c xy dx + \int_c x^2 dy = \int^\frac{\pi}{4}_\frac{-\pi}{4}-cos(t)sin^2(t) +cos^3(t)dt

It seems you have done hard part but stopped at the easy part.
Using identitycos^2^(t)+sin^2(t)=1 write
cos^3(t) = cos(t) (1-sin^2(t)) then substitude
You will find

\int^\frac{\pi}{4}_\frac{-\pi}{4}-2cos(t)sin^2(t) +cos(t)dt

Use the substitution
u=sin(t)

Anyway you will find at the end by substituting sin(\pi/4) = \frac{ \sqrt{2} }{2} integral is equal to \frac{2 \sqrt{2} }{3}


which is not an expected result for you

the reason is the answer of the question (a) is not yes

(a) You did good computations and "computationaly"
your line integrals for r1 and r2 are correct .On the other hand you did mistake in the directions(please look at the attachment) .
For r2 : t does not go from 0 to 1 , it goes from 1 to 0 .
So just multiply by -1 to revert the direction of the integral
As a result sum of the line integrals of r1 and r2 not equal to zero

Conclusion= If you add them all , you get \frac{ \sqrt{2} }{3}