VERY IMPORTANT angular momentum

[fiziksfun]

In the following diagram:

http://i19.tinypic.com/7xaa148.jpg

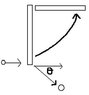
A bullet of velocity 5 m/s hits an initially at rest rod. The mass of the bullet is 2kg.

The rod rotates around its axis in its top, I=(1/3)ML^2. It's mass of 3. It's distance is 4m. The rod finally stops moving after the collision at 90 degrees upward from the collision.

After the collision the bullet moves away at an angle of theta.

Kinetic energy is conserved. I used this to find both both vf and omega f of the bullet and rod.. but

HOW DO I FIND THETA?



any ideas?? PLEASE!?

 

[Nate810]

To find theta, you can use the conservation of angular momentum. The angular momentum of the system before the collision is zero, since the rod is initially at rest. The angular momentum of the system after the collision is the angular momentum of the bullet plus the angular momentum of the rod. Assuming the bullet and rod move in the same direction, the angular momentum of the system after the collision is: L = mv * r + (1/3)ML^2ω where m is the mass of the bullet, v is its velocity, r is the distance from the center of mass of the rod to the point of collision, M is the mass of the rod, and L is the length of the rod. The angle theta is then determined by the ratio of the angular momentum of the bullet and rod, since the total angular momentum must remain constant: theta = arctan(mv * r / (1/3)ML^2ω) You can then use the values for v, M, L, and ω calculated from the conservation of kinetic energy to solve for theta.

 

[ogb p]

Based on the diagram and information provided, it appears that the bullet collides with the rod at a certain angle and then moves away at a different angle, theta. To find theta, we need to consider the conservation of angular momentum.

Angular momentum is defined as the product of an object's moment of inertia and its angular velocity. In this case, we can calculate the initial angular momentum of the system before the collision using the equation L = Iω, where L is the angular momentum, I is the moment of inertia, and ω is the angular velocity.

Since the rod is initially at rest, its initial angular momentum is zero. Therefore, the initial angular momentum of the system is simply the angular momentum of the bullet, which can be calculated as L = Iω = (1/3)ML^2 * ω, where M is the mass of the bullet and L is the distance from the axis of rotation to the point of impact.

After the collision, the bullet moves away at an angle of theta, which means that its final angular momentum is now L = Mvfb * L * sin(theta), where vfb is the final velocity of the bullet. Meanwhile, the rod is rotating at an angular velocity of ωf, so its final angular momentum is L = Iωf = (1/3)ML^2 * ωf.

Since angular momentum is conserved, we can equate the initial and final angular momenta and solve for theta. This gives us the equation:

(1/3)ML^2 * ω = Mvfb * L * sin(theta) + (1/3)ML^2 * ωf

Solving for theta, we get:

sin(theta) = [(1/3)ML^2 * ω - (1/3)ML^2 * ωf] / [Mvfb * L]

Now, we can plug in the values given in the problem to solve for theta. However, since we do not have the values for the final angular velocity of the rod (ωf) and the final velocity of the bullet (vfb), we cannot determine the exact value of theta. We would need to know additional information or make certain assumptions to solve for these variables.

In summary, to find theta, we need to use the conservation of angular momentum equation and plug in the relevant values. However, without knowing the final angular velocity of the rod and the final