nikosb
- 29
- 1
I am working on a project where I have to project a logo on a very narrow angle like shown below:

The projection distance will vary between 6-10 yards and at 10 yards the projected diameter will not be larger than 12inches so the beam angle needs to be less than 5 degrees. The idea is to have a very bright and focused light that can be seen in bright environments, is small and hand held. For example I have a $10 flashlight off ebay that uses a CREE XM-L LED and an aspheric lens that produces a very collimated light and can be seen in lighted environments:

I could use a larger aspheric lense and narrow the projection angle down to 5 degrees but it will always project the shape of the LED emitter. I could de-dome the LED and place a glass gobo directly on top of the LED so as to project gobos with the LED shaped beam as the background. However LED measures only 5x5mm and I am not sure the glass gobo can have very fine details on such a small size.
I have seen somewhere else this schematic for gobo projection:
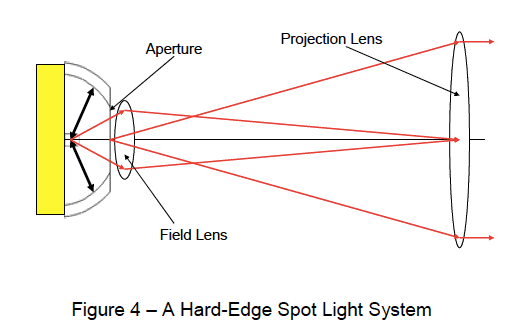
but I don't understand how it works. Supposedly you place the gobo with the image right at the aperture and before the field lens. I don't know what type of lens the field lens is (double convex, plano convex), what the focal distances of either lenses should be, and if this setup could even produce a very narrow beam?
I found some more things online, like this video on youtube, and this webpage showing how to convert a flashlight into a gobo projector albeit with a wide projection angle but I want to understand the physics and see if I can custom make something for my needs. Any advice on what lenses or setup could work for my project?
The projection distance will vary between 6-10 yards and at 10 yards the projected diameter will not be larger than 12inches so the beam angle needs to be less than 5 degrees. The idea is to have a very bright and focused light that can be seen in bright environments, is small and hand held. For example I have a $10 flashlight off ebay that uses a CREE XM-L LED and an aspheric lens that produces a very collimated light and can be seen in lighted environments:
I could use a larger aspheric lense and narrow the projection angle down to 5 degrees but it will always project the shape of the LED emitter. I could de-dome the LED and place a glass gobo directly on top of the LED so as to project gobos with the LED shaped beam as the background. However LED measures only 5x5mm and I am not sure the glass gobo can have very fine details on such a small size.
I have seen somewhere else this schematic for gobo projection:
but I don't understand how it works. Supposedly you place the gobo with the image right at the aperture and before the field lens. I don't know what type of lens the field lens is (double convex, plano convex), what the focal distances of either lenses should be, and if this setup could even produce a very narrow beam?
I found some more things online, like this video on youtube, and this webpage showing how to convert a flashlight into a gobo projector albeit with a wide projection angle but I want to understand the physics and see if I can custom make something for my needs. Any advice on what lenses or setup could work for my project?