I Vibrating String: Blue & Red Line Resonance

[Samson4]

The blue and red lines represent a very stiff string The blue section is plucked and oscillates. The vibration energy is carried through to the red section.

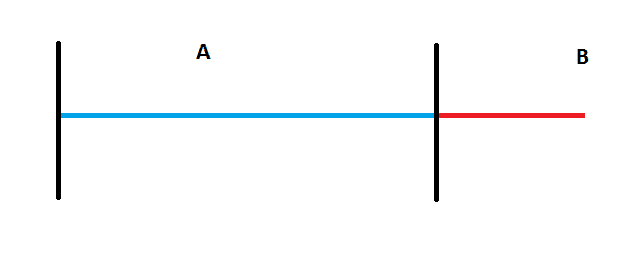
This is what I don't understand.
A) Is the red section a forced oscillation at the resonant frequency of the blue section?
B) Will the vibrations in the blue string drive and dampen the resonant frequency of the red section?

 

[sophiecentaur]

We need a few more details, I think. You will have to explain what the line between A and B represents. How is the A section couples to B section? Are the strings of the same linear density and radius?

 

[rumborak]

@sophiecentaur If I understand the setup correctly, the blue and red sections are just part of a single string. However, the black divider forces a node at that position (by blocking any transversal motion), and essentially only longitudinal stress is transmitted between the two sections.

I don't know actually what the answer is. It might be rather complex behavior since the blue section will certainly be influenced by the red pull, but since it's only longitudinal, it might distort the simple sine wave.

 

[Samson4]

@sophiecentaur If I understand the setup correctly, the blue and red sections are just part of a single string. However, the black divider forces a node at that position (by blocking any transversal motion), and essentially only longitudinal stress is transmitted between the two sections.

I don't know actually what the answer is. It might be rather complex behavior since the blue section will certainly be influenced by the red pull, but since it's only longitudinal, it might distort the simple sine wave.

Exactly, it is one string. If the blue line is plucked, wouldn't the red section experience transverse vibrations as well? Especially if the black lines are sufficiently thin?

 

[rumborak]

That's what I mean, it will be a complex interplay between the blue section that experiences a transversal wave and the red section that will be longitudinal only. I'm not sure there will be an easy answer.

 

[Khashishi]

I assume B is attached to something on the other end, and the resonant frequency of B is different than for A.
I assume the coupling is weak.
When you initially pluck A, you put in energy into many modes. But most of the modes other than the resonant modes die out very quickly due to some dissipation. Some of that energy bleeds into B. The modes in B also dissipate quickly, except for some resonant modes of B.

Barring some nonlinear effects, the modes driven in B are the same frequencies as the modes present in A. Initially, you have many frequencies, with energy at each frequency decreasing exponentially. B acts like a driven damped oscillator, with the driver being all the modes of A with some energy,

 

[jbriggs444]

Exactly, it is one string. If the blue line is plucked, wouldn't the red section experience transverse vibrations as well? Especially if the black lines are sufficiently thin?

A typical "string" supports tension only. It offers no resistance to compression or bending. But what you appear to have in mind is a string with stiffness -- one that resists bending. Something like a fishing rod. Yes, if this is the case and assuming that the junction between A and B is pretty much a hole in a wall then the bending moment from the one section can and will influence the other section.

 

[Samson4]

A typical "string" supports tension only. It offers no resistance to compression or bending. But what you appear to have in mind is a string with stiffness -- one that resists bending. Something like a fishing rod. Yes, if this is the case and assuming that the junction between A and B is pretty much a hole in a wall then the bending moment from the one section can and will influence the other section.

This is what I was trying to articulate. I assumed that the vibration energy could pass through one of these "holes" and drive the other section. If the resonant frequency of A is much lower than B, would plucking A drive B at the resonant frequency of A?

 

[Khashishi]

If the resonant frequency of A is much lower than B, would plucking A drive B at the resonant frequency of A?

Yeah. But in a driven damped oscillator, if you drive far off resonance, you get very little amplitude.
Now, strings are slightly nonlinear. If you pluck the string hard, the string has to lengthen a little bit to become displaced vertically. So, maybe this can cause the frequencies to mix slightly and put a small amount of energy at the B resonant frequency.

Real world example: the bridge of a violin. I've plucked the short string below the bridge. It doesn't do much to the long string. Not enough amplitude to actually hear.

 

[sophiecentaur]

This is what I was trying to articulate. I assumed that the vibration energy could pass through one of these "holes" and drive the other section. If the resonant frequency of A is much lower than B, would plucking A drive B at the resonant frequency of A?

I would see it as the section B loading the section A and affecting the overall resonance. For a short length of B, B could be replaced by a mass (A so called lumped component) In that case it would just lower the frequency. If B were half the length of A, I would expect the resonant frequency of B to be the same as that of A. Like an open ended organ pipe, attached to a closed pipe.
This would be more straightforward if, rather than being plucked, the system was excited with a single frequency from a sinusoidal driver, loosely coupled to it. You would then only be considering a single overtone. Plucking always introduces a load of frequencies due to all the overtones that are excited by the triangular shape during plucking.

 

[Samson4]

I would see it as the section B loading the section A and affecting the overall resonance. For a short length of B, B could be replaced by a mass (A so called lumped component) In that case it would just lower the frequency. If B were half the length of A, I would expect the resonant frequency of B to be the same as that of A. Like an open ended organ pipe, attached to a closed pipe.
This would be more straightforward if, rather than being plucked, the system was excited with a single frequency from a sinusoidal driver, loosely coupled to it. You would then only be considering a single overtone. Plucking always introduces a load of frequencies due to all the overtones that are excited by the triangular shape during plucking.

So there would only be one resonant frequency for the whole system? Much like that of a mass and spring? B taking the place of the mass?

 

[Nidum]

If the 'string' has significant bending stiffness then this is a simple problem of beam vibration .

Beam with a pin support at one end and another pin support inboard from the other end .

The whole beam vibrates and it will have a range of natural frequencies and mode shapes .

Problem of this type can be analysed by standard means .

 

[olivermsun]

Interestingly, piano strings are a common example of a string with nontrivial stiffness. There are a bunch of discussions out there that can be found with a literature search (even Feynman was apparently interested in this topic!). Essentially, the wave equation has to be modified to account for the stiffness.

However, for this problem there seem to be some different assumptions being made that would change the approach the problem. For example, why is the wave in the red section assumed to be longitudinal only? Even if the divider prevents transverse displacements (it creates a node), doesn't that still allow the possibility that the (stiff) string can cross the boundary at an angle, thereby transmitting longitudinal waves to the other side?

(My point is, the exact boundary condition needs to be specified.)

 

[Samson4]

Interestingly, piano strings are a common example of a string with nontrivial stiffness. There are a bunch of discussions out there that can be found with a literature search (even Feynman was apparently interested in this topic!). Essentially, the wave equation has to be modified to account for the stiffness.

However, for this problem there seem to be some different assumptions being made that would change the approach the problem. For example, why is the wave in the red section assumed to be longitudinal only? Even if the divider prevents transverse displacements (it creates a node), doesn't that still allow the possibility that the (stiff) string can cross the boundary at an angle, thereby transmitting longitudinal waves to the other side?

(My point is, the exact boundary condition needs to be specified.)

I didnt understand that either. I assumed that the vibrations would pass into red with little dampening if the contact at the node was both sufficiently small and stiff.

 

[sophiecentaur]

I didnt understand that either. I assumed that the vibrations would pass into red with little dampening if the contact at the node was both sufficiently small and stiff.

It would be necessary to quantify quite a few parameters.
You could investigate the way that quartz crystal oscillators are manufactured. They are often built a bit like your diagram - but with a short 'B' section each end. They manage to get those little devils right so it's all be sorted by someone, at least.