Why does a guitar string "beat" as if it is out of phase?

[mikejm]

I am working on synthesis modelling of guitars, and I have managed to capture most elements of the guitar well so far.

Something I am struggling to understand is why a guitar string has a natural "beating" sound to it, meaning it sounds as if it is ebbing and flowing slowly as it vibrates.

To illustrate what I mean, here is a sound file of a guitar string plucked once:

https://filebin.net/wo4borxaxe74nbg2

If you listen, it sounds as if the pitch is almost slowly fluctuating up and down over time, or the volume is increasing and decreasing.

I have done a pitch analysis, and it doesn't appear to be a true pitch fluctuation:

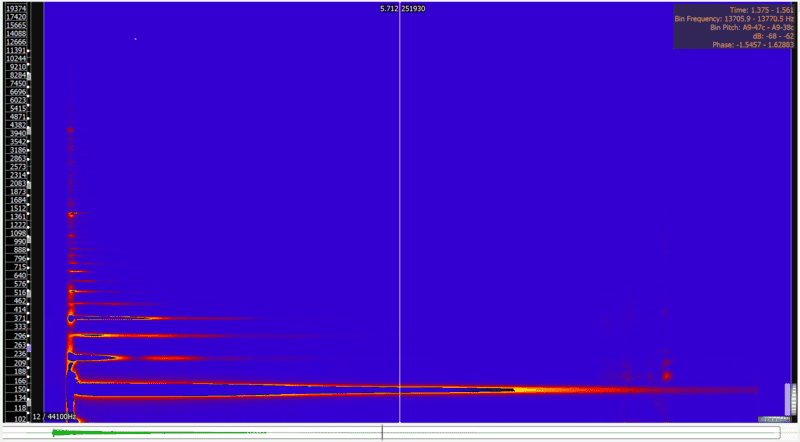
The fundamental note and harmonics all appear to have a very steady pitch over time.

However, what can be seen particularly with the second harmonic is that this harmonic comes and goes in intensity over the duration of the note. All the higher harmonics can be easily seen to do this.

It would appear this is what creates the "ebbing and flowing" sound.

I found one post online which seemed to try to explain this behavior:

"Unlike the ideal mathematical model, strings vibrate in two dimensions. Since the change in tension is more pronounced in one dimension than the other, we're actually hearing two sounds. This causes some harmonics to get canceled while others become more pronounced. As the frequencies of these two vibrations shift relative to each other, the harmonics that get canceled or become pronounced also change. This causes a slight chorusing or flanging effect. It's also an inherent limitation of plucked string instruments but it's also OK, it's also part of the sound we know and love."

https://music.stackexchange.com/que...-a-guitar-why-is-it-only-in-tune-for-a-moment

I am wondering if this is the correct explanation for why this happens? If so, can anyone elaborate further?

I am trying to understand what they mean by the string "vibrating in two dimensions" or how this creates this phasing/chorusing/flanging effect.

Thanks.

 

[Mister T]

My guess is that the vibrating string and the guitar cavity form a pair of coupled oscillators, with energy being swapped back and forth between them.

 

[sophiecentaur]

The so-called harmonics are not actual harmonics. The Overtones of the string are not necessarily exact harmonics and the few Hz (or less) difference between the string overtones and any harmonics or other overtones could account for this effect.
Although an ideal string will have overtones that are harmonically related, both ends of the string are not well defined (particularly the finger on fret end). The timbre of all instruments is 'attractive' for this sort of reason.

 

[Steelwolf]

Another point is that the string is not plucked at it's center either, it is off on one end, so the counter vibration would be at the other end of the string, same distance from the end, so that there is a harmonic caused by the exact place it is plucked. Usually this is nowhere near noticeable, but with our extremely precise electronics we are able to discern things that are just beyond human hearing. Some folks can hear these minor differences but most never hear or consider them.

 

[sophiecentaur]

most never hear or consider them

They just appreciate something 'different' between two different stringed instruments and between individual instruments of the same kind. Id musical sounds were just based Hammond Organ style mixes of harmonics, life would be far less rich.

 

[slow]

I am working on synthesis modelling of guitars

If the structure of the guitar has a non-negligible degree of flexibility, for example guitar with box or half box, there are 3 dimensions in the vibration of the string. The diapason lever on the box and the length of the string varies. that is a dimension, which corresponds to the longitudinal vibration.

The other two are transverse and you can express them with two components, for example a coordinate transverse to the string and parallel to the plane of the box another perpendicular to that plane.

The 3 components contribute to varying the tension of the strig and to leverage on the box, causing pitching. Stationary waves occur in the material of the guitar, which last for a time before the energy of those waves dissipates in heat. In that time they interfere with the waves of the last sound that has been played on the instrument.

For all that happens exactly what you have described.

The pitching caused by the action of the string on the structure of the instrument is very special, since the frequency of the note varies periodically and the period coincides with the period of the note that sounds. It is a pitching mathematically identical to a wave function, if you formulate the frequency variation as a function of time.

All this gives a very complex, multidimensional phenonenon, that is, it requires using many variables to formulate an adequate description. If you manage to well synthesize the sound of the guitar, you would make a very worthy contribution.

 

[mikejm]

The so-called harmonics are not actual harmonics. The Overtones of the string are not necessarily exact harmonics and the few Hz (or less) difference between the string overtones and any harmonics or other overtones could account for this effect.
Although an ideal string will have overtones that are harmonically related, both ends of the string are not well defined (particularly the finger on fret end). The timbre of all instruments is 'attractive' for this sort of reason.

What you're referring to is the inharmonicity of the harmonics. I have accounted for that in my design, and it is very important for the instrument, but it does not create the "beating" tone that we are referring to.

 

[mikejm]

Another point is that the string is not plucked at it's center either, it is off on one end, so the counter vibration would be at the other end of the string, same distance from the end, so that there is a harmonic caused by the exact place it is plucked. Usually this is nowhere near noticeable, but with our extremely precise electronics we are able to discern things that are just beyond human hearing. Some folks can hear these minor differences but most never hear or consider them.

Off center plucking creates nodes and antinodes which will then mute or emphasize certain modes (harmonics) of vibration. But to my knowledge, this shouldn't cause harmonics to fluctuate in intensity over the duration of the sound (ie. pulse or beat as shown here).

 

[sophiecentaur]

but it does not create the "beating" tone that we are referring to.

Have you actually measured this or are you just making an assertion?
If you look at a scope trace of a guitar note, you can very often (always?) see a steady, low frequency, which is what the scope triggers on but also you see higher frequency patterns which march along the fundamental stationary pattern. If all the components were harmonics, this wouldn't happen and the pattern would be stable - just decaying in amplitude - and that implies inharmonicity. Just how the ear makes sense of this is difficult to predict but it is not ridiculous to suggest that a beat pattern would be perceived where the beats are between the overtones and genuine harmonics, generated elsewhere - even in the hearing process.

 

[mikejm]

Have you actually measured this or are you just making an assertion?
If you look at a scope trace of a guitar note, you can very often (always?) see a steady, low frequency, which is what the scope triggers on but also you see higher frequency patterns which march along the fundamental stationary pattern. If all the components were harmonics, this wouldn't happen and the pattern would be stable - just decaying in amplitude - and that implies inharmonicity. Just how the ear makes sense of this is difficult to predict but it is not ridiculous to suggest that a beat pattern would be perceived where the beats are between the overtones and genuine harmonics, generated elsewhere - even in the hearing process.

I have synthesized harmonics in a guitar like pattern with inharmonicity applied and no beating similar to this occurs. Each harmonic rings independently at the level that is requested. But that may be a limitation of my synthesis. Audio synthesis is not the same as true physical modelling like Ansys. It's just doing what I tell it to.

But if you do modeling of a simple string with Ansys, I do not think it will predict beating from what I've seen, though I'm not good with Ansys. It will however give inharmonicity, so I don't think inharmonicity is directly the cause.

eg.


Just because the harmonics are not exact multiples (inharmonic) does not mean they will beat automatically. Or does it? I can't see how that would make sense. If inharmonic modes automatically lead to beating, then wouldn't there be beating present in every vibrational analysis of any object (since nothing in nature is perfectly harmonic)? Or is there?

It seems more to me like this must be something to do with the guitar body and feedback between the string and the body causing some phasing or other cancellation of the harmonics periodically. I will post an example a bit later, but when you apply a "chorus" effect, it can somewhat simulate what we see here. A chorus effect is typically done by adding a slightly off-pitched version of the audio to the original audio which creates beating. But it can also be done by directly shaping the harmonic levels in an oscillating manner.

I'm just not sure exactly why those harmonic amplitude oscillations occur in the real world.

 

[olivermsun]

If the overtones are not "true" harmonics (exact multiples), then how can they not beat? The phase relationship between the overtones and the fundamental cannot be fixed because they have different periods, e.g., the overtones and the true harmonics are slightly off-pitch. In fact, the overtones are recognizable as such because they are nearly exact multiples, hence the beat frequency tends to be low and quite apparent.

 

[sophiecentaur]

If the overtones are not "true" harmonics (exact multiples), then how can they not beat? The phase relationship between the overtones and the fundamental cannot be fixed because they have different periods, e.g., the overtones and the true harmonics are slightly off-pitch. In fact, the overtones are recognizable as such because they are nearly exact multiples, hence the beat frequency tends to be low and quite apparent.

That's my problem, too. But the uncertainty about this is surely due to the use of a simulator. The results of a simulator are only as good as the simulation itself. If, as it seems, the simulation does not throw up the same beats as the guitar then it is not up to the job. Simulation is no more than a convenient calculation which relies on accurate modelling and it is very risky to do 'research' using simulations unless they have been thoroughly tested in the context of the particular research field. That should be step number one in selection to use an off the shelf simulation.
One thing the OP seems to have revealed is that the beating is not psycho-audio because I understand that he has listened to the result. This assumes that the audio quality was good enough. For instance, it would be necessary to compare recorder guitar notes and the synthesised version.

"the overtones are recognizable as such because they are nearly exact multiples, hence the beat frequency tends to be low and quite apparent". I would have thought that the overtones could well be generated within the ear but the resonant / matching parts of the body could well be non linear enough to generate intermodulation products in their own right and that may cause the beats that we 'hear'.