- #1
Koscher
- 22
- 0
Homework Statement
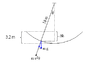
Tarzan, who weighs 618 N, swings from a cliff at the end of a convenient vine that is 18.0 m long (see the figure). From the top of the cliff to the bottom of the swing, he descends by 3.2 m.
A. If the vine doesn't break, what is the maximum of the tension in the vine? 837.733 N
B. The vine will break if the force on it exceeds 730.9 N. Does the vine break? If yes, at what angle does it break (if no enter 180. deg)?
So i solved part A, what I am asking about is part B.
2. The attempt at a solution
The first time I attempted the problem:
T=mg+m(v2/R)
T=mg+m(2gh/R)
730.9 N = 618 N + (2*618*h)/18
h=1.64417 m
cos(θ)=(L-h)/L=(18-1.64417)/18
θ=24.68°
The second time i attempted it, I realized that the vine would break at a point that would still have potential energy as well as kinetic energy.
mgh22+(1/2)mv^2=mgh1
T=mg+m([2(gh1-gh2)/R)
Then plugged in values and solved for h2, which resulted in 1.5583 m.
cos(θ)=(L-h)/L=(18-1.5583)/18
θ=23.997°
Does that seem to be on the right track? or is it completely wrong?