Vine breaks during tarzan's swing at what angle?

[Koscher]

Homework Statement

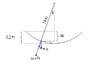
Tarzan, who weighs 618 N, swings from a cliff at the end of a convenient vine that is 18.0 m long (see the figure). From the top of the cliff to the bottom of the swing, he descends by 3.2 m.

A. If the vine doesn't break, what is the maximum of the tension in the vine? 837.733 N

B. The vine will break if the force on it exceeds 730.9 N. Does the vine break? If yes, at what angle does it break (if no enter 180. deg)?

So i solved part A, what I am asking about is part B.

2. The attempt at a solution

The first time I attempted the problem:

T=mg+m(v²/R)
T=mg+m(2gh/R)
730.9 N = 618 N + (2*618*h)/18
h=1.64417 m
cos(θ)=(L-h)/L=(18-1.64417)/18
θ=24.68°

The second time i attempted it, I realized that the vine would break at a point that would still have potential energy as well as kinetic energy.

mgh₂2+(1/2)mv^2=mgh₁
T=mg+m([2(gh₁-gh₂)/R)

Then plugged in values and solved for h₂, which resulted in 1.5583 m.
cos(θ)=(L-h)/L=(18-1.5583)/18
θ=23.997°

Does that seem to be on the right track? or is it completely wrong?

 

[gneill]

You'll need an expression for the velocity with respect to angle (so, change in height gives the change in potential energy which leads to the velocity). Next, note that the centripetal force lies along the direction of the vine already. In terms of contribution to tension you can depict that as a centrifugal force at the end of the vine. Added to that will be the portion of the gravitational force that also lies along that vector.

 

[Koscher]

I need to find an expression for velocity with respect to the angle? So when I am making this equation, will i need to take into account an angle with the Weight of Tarzan as well? I also know that I can make v^2=2gh. If I then used trig to find a relationship between h and the angle, such as h=R-Rcosθ. Would a method like that work?

 

[gneill]

I need to find an expression for velocity with respect to the angle? So when I am making this equation, will i need to take into account an angle with the Weight of Tarzan as well? I also know that I can make v^2=2gh. If I then used trig to find a relationship between h and the angle, such as h=R-Rcosθ. Would a method like that work?

Sure, use the potential energy change from the initial height to the current position in order to determine the kinetic energy and hence the velocity. Make sure that you're calculating the drop in height rather than the height above the nadir of the arc.

 

[Koscher]

Okay. So i got:

PEi + KEi = PEf + KEf
mgh₁ + 0 = (1/2)mv² + mgh₂
-----v²=2gh₂-----Substituted in the above formula
mgh₁ = mgh₂ + mgh₂
gh₁ = 2gh₂
h₂ = 1.6 m

THEN:

PEi = PEf + KEf

Solve for v.
v= 5.60285 m/s

Now I need to use velocity to find the angle correct?

 

[gneill]

Okay. So i got:

PEi + KEi = PEf + KEf
mgh₁ + 0 = (1/2)mv² + mgh₂
-----v²=2gh₂-----Substituted in the above formula
mgh₁ = mgh₂ + mgh₂
gh₁ = 2gh₂
h₂ = 1.6 m

THEN:

PEi = PEf + KEf

Solve for v.
v= 5.60285 m/s

Now I need to use velocity to find the angle correct?

It's difficult to follow your logic when the variables (such as h1 and h2) are not defined. Even so, it should be clear that you need an expression for the velocity not a particular value, since the centripetal force will vary as the velocity does.

Essentially, you need an expression for the tension as a function of θ. This is comprised of the centripetal force and the component of the gravitational force that is aligned with it. The centripetal force depends upon the velocity, which in turn depends upon the gravitational PE converted to KE.

 

[Koscher]

I apologize for taking up your time, but I really am lost when it came to this question. But if i know that:

ΔPE=ΔKE
mgLcosθ=(1/2)mv²
v²=2gLcosθ

So:

T-mgcosθ=ma
T-mgcosθ=m(v²/L)
T-mgcosθ=2gcosθ
T=3mgcosθ

Am I on the right track? I would not even be offended if you said no.

 

[gneill]

The distance by which Tarzan drops is not Lcosθ. Remember that the radius of the circle that he follows is 18m, yet his total drop is only 3.2m. So he only follows a small arc of the circle.

You'll need to further analyze the diagram in order to determine the extent of his descent with respect to angle.

If the arc radius is r = 18m and the total drop in height is h = 2.3m, then the drop as a function of angle (from vertical) is:

$\Delta h = r\;cos(\theta) - (r - h)$

 

[Koscher]

Okay, now I'm lost. When I plugged the value in i got:

T=mgcosθ+(mg(L-Lcosθ)L)

But with algebra terms cancel out until only T=mg is left.

 

[gneill]

Okay, now I'm lost. When I plugged the value in i got:

T=mgcosθ+(mg(L-Lcosθ)L)

But with algebra terms cancel out until only T=mg is left.

Can you show the steps you used to get to that point? What does the centripetal force term look like?

 

[Koscher]

OH! I just figured it out! I am hesitant to put how to do it on here, that way when other people are trying to do the problem they will also have to go through the steps in order to figure it out. I know the method is correct because the angle that I got as an answer, I submitted to my online homework program and it was correct. Thank You very much for helping me, you helped more than you know.