Visual Proofs in Mathematics: Does Pictures Tell More than 1000 Words?

[dextercioby]

People usually say that pictures tell more than 1000 words. Is that still true in mathematics...? I think so. Let me first say what i mean by 'visual proof'. Let's say we have an identity. To prove it's true one may write from a line to more than one page. But what if one was able to write only one formula instead of the whole proof and let the eyes and the mind "figure it out".

Here's what i mean. The sine and cosine addition formulas are a mess to prove in elementary trigonometry. However, i'd say that

\displaystyle{e^{i\left(x+y\right)} =e^{ix} e^{iy}}

is a "visual proof". Basically an agile mind and some healthy eyes would "get it" without feeling the need to grab the pencil & do the calculations involved.

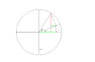
Going further, using the same task (proving the addition formulas for sine & cosine), one could literally come up with a picture, like this one attached below.

So what do you think of my idea? Is it dumb? If not, could you come up with some of your own results...?

Daniel.

 

[nocturnal]

Theres actually a book (or a whole series of books) called "Proofs without words" (or something like that) which is a collection of "visual proofs" as you describe them. As an example, they give pictorial arguments "proving" Pythagoras' Theorem using nothing but pictures of different sizes of triangles and quadrilaterals stacked next to each other.

I glossed through one once and it was fun to look at. Although it was valuable at building one's intuition, I still wouldn't call it a proof until it can be made rigorous by today's standards.

 

[nocturnal]

Ah, here we go:
https://www.amazon.com/gp/product/0883857006/?tag=pfamazon01-20

 

[robphy]

The American Mathematical Monthly http://www.maa.org/pubs/monthly.html
and the College Mathematics Journal http://www.maa.org/pubs/cmj.html
occasionally publish "proofs without words".
You might try to submit yours.

 

[cliowa]

So what do you think of my idea? Is it dumb?

Calling it dumb is going a little too far, I feel. Oversimplifying is quite a good description, in my opinion. Let me explain.
In my opinion the rigour in formulation and execution which mathematics achieves is one, if not the, great thing about mathematics. One of the miracles is that this abstractly developed formalism helps us describe nature in very precise ways.
Elementary mathematics is based to a large extent on intuition. Many of the great mathematicians of the past have not exercised mathematics with the same accuracy that is applied today (I'm referring to Euler, Bernoulli and many others; they used their intuition quite often). Another beauty of (simpler) mathematics is a kind of dualism: There is in most cases a very intuitively pleasing visualization which hugely HELPS understanding things better. However, this does not substitute for understanding ideas, proofs. The problem is: Our intuition, visualizations can be utterly wrong. When visualizing ideas we usually simplify and concentrate on main aspects, which is good for this purpose. But take as an example peano curves: One's personal intuition can be totally misleading. I mean to say that visual proofs are not proofs, simply because our mind doesn't naturely think in a precise step-by-step way, as it should for mathematical purposes.

What you call visual proofs I would therefore refer to as visual hints. A trained mathematician has a mathematically trained eye, which helps him grasp connections better. If you show your sine/cosine-stuff to a trained person, he/she will immediately and completely automatically have lots of thoughts, faster than pronouncable, that will lead him/her to a certain conclusion amazingly fast. But again: That's training. As I feel this is mainly taking place when combining well-known things (of course) it helps understanding/ demonstrates understanding. To a newbie the picture you draw would seem comprehensible, but would not help him/her with developping important mathematical abilities (which are needed when there is no easy illustration). To a pro your drawing would be a welcome backup. But nothing more than that, in my opinion.
Best regards...Cliowa

P.S.: Of course there are also areas in mathematics where proofs are done by construction on paper. Trivially, there visual proofs are proofs.

 

[fourier jr]

Theres actually a book (or a whole series of books) called "Proofs without words" (or something like that) which is a collection of "visual proofs" as you describe them. As an example, they give pictorial arguments "proving" Pythagoras' Theorem using nothing but pictures of different sizes of triangles and quadrilaterals stacked next to each other.

I glossed through one once and it was fun to look at. Although it was valuable at building one's intuition, I still wouldn't call it a proof until it can be made rigorous by today's standards.

i would have to agree here. maybe the title should say "proofs" rather than proofs (without the "". i imagine a good exercise would be to work through a book like that looking at the pictures, figuring out what is to be proved, and then writing a REAL proof of what the picture is intended to show. i wouldn't consider a picture alone to be a true proof, but perhaps something someone could use to grasp or illustrate what a theorem states.