- 11,326
- 8,754
I promised to work an example to explore whether using a square wave rather than a sin wave might make AC circuits easier to explain to beginners. As an old time analog guy, I always learn best from study of time plots. 
Before showing the results, my conclusion is that the answer to the square wave experiment is "No.. Not useful." A square wave allows one to dodge the fuzzy idea of phase angle, but the spiky plots are just too hard to follow.
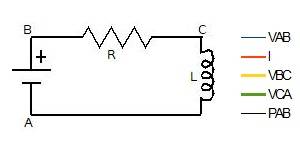
I made a numerical example using an RL circuit. Below is the circuit. Note that I labeled the nodes A B and C. On the right is the color legend for the time plots below. Do not get confused by the sign conventions. VAB+VBC+VCA=0 using these sign conventions.
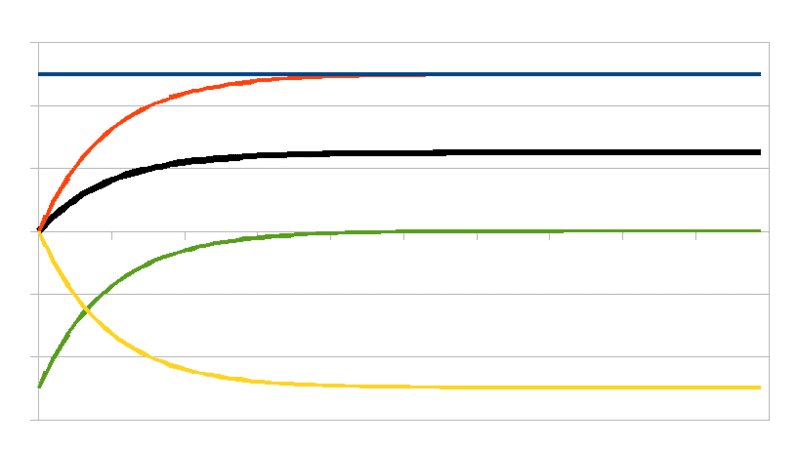
First, below is a familiar DC step response. Time is the horizontal axis. Initial conditions were all zero. At time t=0+, the current is zero and all the voltage drop is across the inductor. In the steady state the voltage across the inductor, VCA, is zero. The ratio R/L is 10.
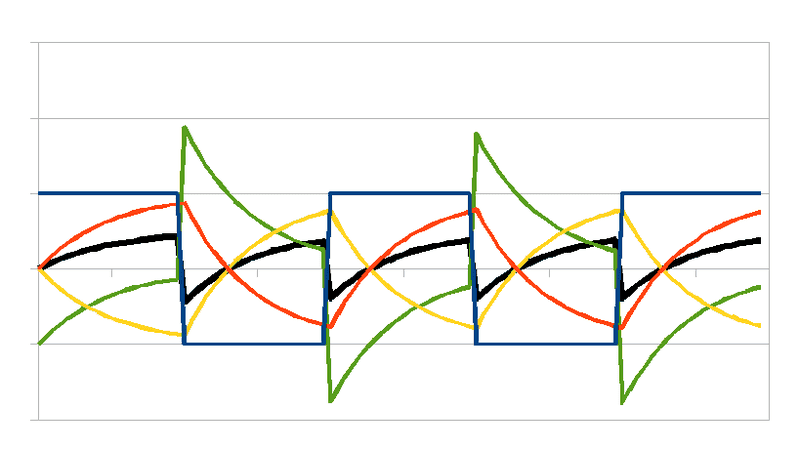
Now below see the same circuit's response to 2.5 cycles of a square wave in VAB. It approximates AC but not exactly because there are not enough cycles shown to wipe out the arbitrary initial conditions. The power PAB can be seen to be both positive and negative during a single cycle. We also see that the times of current zeroes and voltage zeroes are not the same. That was the misunderstanding of the OP in this thread.
If the time integral of power flow over a whole cycle is exactly zero, we say that the AC power is purely imaginary. (@sophiecentaur, the word imaginary comes from the complex number descriptions of this circuit. Blame the history of mathematics, not the history of EE for the word choice.)
I like to stress that P=VI instantaneously always works for both DC and AC. The only time when AC is different from DC is when we define AC values as averages over a whole cycle (and many cycles after the startup transients have died away.) IMO, if we stressed that more emphatically, then students would have less difficulty in going from DC to AC learning.
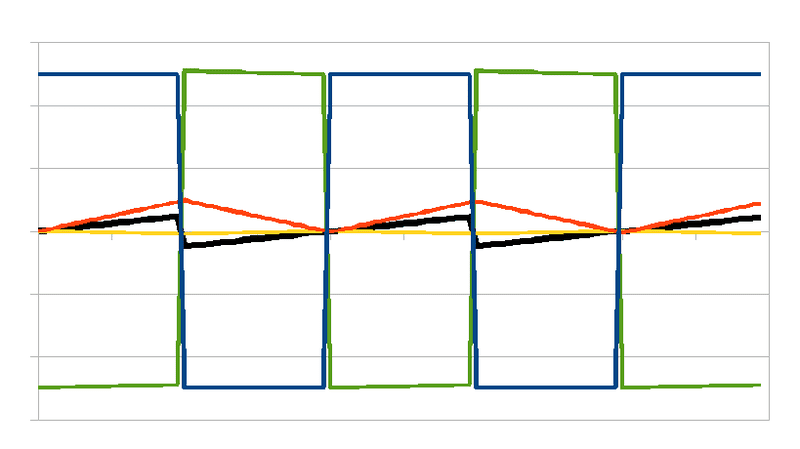
Finally, see below the same 2.5 cycles, but changing the values of R and L so that R/L is 0.1 instead of 10.0. With those numbers, the voltage across the inductor approximates the same square wave as VAB but shifted one half cycle. Current maximums are roughly 90 degrees out of phase with the square wave. Current wave shape looks like a triangle wave and power looks like a sawtooth.
 p.s. I also did the case with a capacitor instead of an inductor, but I didn't upload them because I think the whole exersize (while fun) is of no value. If someone disagrees and asks, I'll post those too.
p.s. I also did the case with a capacitor instead of an inductor, but I didn't upload them because I think the whole exersize (while fun) is of no value. If someone disagrees and asks, I'll post those too.
Before showing the results, my conclusion is that the answer to the square wave experiment is "No.. Not useful." A square wave allows one to dodge the fuzzy idea of phase angle, but the spiky plots are just too hard to follow.
I made a numerical example using an RL circuit. Below is the circuit. Note that I labeled the nodes A B and C. On the right is the color legend for the time plots below. Do not get confused by the sign conventions. VAB+VBC+VCA=0 using these sign conventions.
First, below is a familiar DC step response. Time is the horizontal axis. Initial conditions were all zero. At time t=0+, the current is zero and all the voltage drop is across the inductor. In the steady state the voltage across the inductor, VCA, is zero. The ratio R/L is 10.
Now below see the same circuit's response to 2.5 cycles of a square wave in VAB. It approximates AC but not exactly because there are not enough cycles shown to wipe out the arbitrary initial conditions. The power PAB can be seen to be both positive and negative during a single cycle. We also see that the times of current zeroes and voltage zeroes are not the same. That was the misunderstanding of the OP in this thread.
If the time integral of power flow over a whole cycle is exactly zero, we say that the AC power is purely imaginary. (@sophiecentaur, the word imaginary comes from the complex number descriptions of this circuit. Blame the history of mathematics, not the history of EE for the word choice.)
I like to stress that P=VI instantaneously always works for both DC and AC. The only time when AC is different from DC is when we define AC values as averages over a whole cycle (and many cycles after the startup transients have died away.) IMO, if we stressed that more emphatically, then students would have less difficulty in going from DC to AC learning.
Finally, see below the same 2.5 cycles, but changing the values of R and L so that R/L is 0.1 instead of 10.0. With those numbers, the voltage across the inductor approximates the same square wave as VAB but shifted one half cycle. Current maximums are roughly 90 degrees out of phase with the square wave. Current wave shape looks like a triangle wave and power looks like a sawtooth.
 ).
). ..
.. Gosh, Sophie - THANK YOU SIR !
Gosh, Sophie - THANK YOU SIR !