Volume by Shell and Washer Methods

[rodneyspencer]

Homework Statement

Find the volume generated by rotating the given region about the given line using the Shell method and the Washer method.

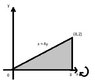
x = 4y [y = x/4], y = 0, x = 0, x = 8 about x

Homework Equations

Washer method (about x):
V = pi \int^b_a ((R_top²(x) - r_bottom²(x))dx

Shell method (about x):
V = 2pi \int^d_c (y[f(y)-g(y)])dy

The Attempt at a Solution

I'm not sure why I can't reconcile these two answers. I'm having some similar problems with more of these exercises but if someone can help me see where I'm going wrong I'm sure I can rework them successfully.

Washer:
V = pi \int^8_0 ((x/4)²)dx = 32pi/3

Shell:
V = 2pi \int^2_0 (y(4y))dy = 64pi/3

 

[rodneyspencer]

I forgot about x=8. The shell method should be V = 2pi \int^2_0 (y(8-(4y)))dy = 32pi/3.

:facepalm:

 

[rodneyspencer]

Double-post :/

:facepalm: