- #1
blackbelt5400
- 17
- 0
Assume that 0<r<R.
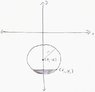
Consider the circle [tex]x^2+(y+R)^2=r^2[/tex]. Obviously, if we revolve this circle about the x-axis, we get a torus whose volume is [tex] (\pi r^2)(2\pi R)[/tex].
Now consider a point [tex] y_1 [/tex] such that R-r<[tex]y_1[/tex]<R. and let [tex] (x_1,y_1) [/tex] be a point on the circle. The volume of the solid formed by revolving the region inside of the circle and below [tex] y_1 [/tex] about the x-axis is
[tex] 2\pi [(R^2+r^2-y_1^2)x_1+R(x_1\sqrt{r^2-x_1^2}+r^2\sin^{-1}{(\frac{x_1}{r})})-\frac{x_1^3}{3}][/tex].
Assume that a storage tank determined by this solid is filled to a height "h". What is V(h)?
I have attempted this in rectangular coordinates, but I don't believe that it's possible to set up an integral with these weird bounds. Changing to shperical or cylindrical coordinates will not work because this would introduce an error when integrating the distance from the origin.
I was told to try toroidal coordinates [tex] (\sigma, \tau, \phi)[/tex], and I have solved for the foci and the constant [tex]\tau [/tex] for this problem, but I don't know how to set up the integral.
Consider the circle [tex]x^2+(y+R)^2=r^2[/tex]. Obviously, if we revolve this circle about the x-axis, we get a torus whose volume is [tex] (\pi r^2)(2\pi R)[/tex].
Now consider a point [tex] y_1 [/tex] such that R-r<[tex]y_1[/tex]<R. and let [tex] (x_1,y_1) [/tex] be a point on the circle. The volume of the solid formed by revolving the region inside of the circle and below [tex] y_1 [/tex] about the x-axis is
[tex] 2\pi [(R^2+r^2-y_1^2)x_1+R(x_1\sqrt{r^2-x_1^2}+r^2\sin^{-1}{(\frac{x_1}{r})})-\frac{x_1^3}{3}][/tex].
Assume that a storage tank determined by this solid is filled to a height "h". What is V(h)?
I have attempted this in rectangular coordinates, but I don't believe that it's possible to set up an integral with these weird bounds. Changing to shperical or cylindrical coordinates will not work because this would introduce an error when integrating the distance from the origin.
I was told to try toroidal coordinates [tex] (\sigma, \tau, \phi)[/tex], and I have solved for the foci and the constant [tex]\tau [/tex] for this problem, but I don't know how to set up the integral.
Last edited: