Washer Method and Shell Method

[stripedcat]

Just doing the Washer Method for now, once that's sorted out I'm going to see if I can do the Shell Method. I just want to be sure I'm doing this right here.

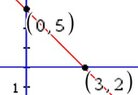
View attachment 2649

That's x=0, y=2, y=5-x

This is around the X-Axis.

R(y) = 5+y, r(y)=2

Assuming that part is at least correct. The integral goes from 2 to 5.

\(\displaystyle \pi \int (5+y)^2 - (2)^2\)
\(\displaystyle y^2+10y+21\)
\(\displaystyle y^3/3+5y^2+21y\)

Then insert 5 and, solve, then the 2, solve, and subtract the 2 result from the 5 result, then the that result times pi?

 

[Deveno]

If you are rotating that region about the $x$-axis, your integral should be along the $x$-axis (using "$dx$").

The outer radius is going to be:

$R(x) = 5 - x$

and the inner radius is going to be:

$r(x) = 2$.

So each washer will have "volume":

$\pi((R(x))^2 - (r(x))^2)\ dx$

From your diagram, it appears we are integrating from $x = 0$ to $x = 3$, so the volume of the solid of revolution is:

$\displaystyle V = \pi\int_0^3 (5 - x)^2 - 4\ dx$

The integral you are trying to work out is revolution about the $y$-axis, so there is some confusion here, but even if it were about the $y$-axis, the integral you have listed is not correct.

 

[magneto1]

One thing that may help is that you draw the cross-section "rectangle" that you are trying to integrate across. If you want to use washer/disk, the rectangle should be perpendicular to the axis of rotation. If you want to use shell method, it should be parallel.

If you evalulate the integral posted by Deveno, you get $27 \pi$.

You can check that if you use the shell method, you get:

\[
2\pi \int_a^b y h(y) dy = 2\pi \int_2^5 y (5-y) dy = 27 \pi
\]

The results are both equal.

 

[stripedcat]

If you are rotating that region about the $x$-axis, your integral should be along the $x$-axis (using "$dx$").

The outer radius is going to be:

$R(x) = 5 - x$

and the inner radius is going to be:

$r(x) = 2$.

So each washer will have "volume":

$\pi((R(x))^2 - (r(x))^2)\ dx$

From your diagram, it appears we are integrating from $x = 0$ to $x = 3$, so the volume of the solid of revolution is:

$\displaystyle V = \pi\int_0^3 (5 - x)^2 - 4\ dx$

The integral you are trying to work out is revolution about the $y$-axis, so there is some confusion here, but even if it were about the $y$-axis, the integral you have listed is not correct.

It actually wants both, I just typo'd the X axis because it was the first one and I was sure on how to do that one.

It's valid for the Y axis then?

 

[Deveno]

If we are rotating about the $y$-axis, we really ought to call it the "disk" method, because we don't have a "hole" in the middle.

In that case, we have: $R(y) = 5 - y$ and our volume element is:

$\pi(R(y))^2 dy = \pi(5 - y)^2\ dy$, so that we have:

$\displaystyle V = \pi\int_2^5 (5 - y)^2\ dy$

which again, is not the integral you originally posted.

 

[stripedcat]

Hrm, well crap, my notes are wrong then. I somehow got the impression that rather than just solving y= 5 - x that you just reversed it, which would make it + instead of -. I'll have to re-watch the lecture.

EDIT: Oh fantastic, the lectures are wrong... Again.

Thank you for the help though. I'll be back once I email the instructor...

Again.

EDIT2:

How in the heck did I get the x-axis rotation right then? I was using faulty information and got lucky? My answer totally agrees with that above 27pi, which is the result of a x^3/3-5x^2+21x with a 3 plugged in for the x value.

And the lecture on arc length seems to have the same error as the shell method video... gah!