Waveforms, rms, average, offsets

[D44]

Hi guys

I'm trying to work out average and rms values of two different waveforms.

One is a sinusoidal wave, the other a ramped trapezoid (I think that's right).

The sinusoidal wave has a peak to peak voltage of 11v and the offset is alleged to be
9-15 = -6v. This is something I've been told to calculate in this way.

So what I have is a sine wave, starting at -6v, reaching a peak at -0.5v and a minimum of -11.5v? Average voltage = -6v? Rms = -0.5/sqrt(2) = -0.35v?? That isn't right, I know. Any help?

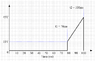
Now, the trapezoid...

Von = 11v, Voff = 45v, Ton = 0.022s.

Am I right in thinking...

For the triangular part (splitting the wave into a square and a triangle), I have Vave = 11+((45-11)/2) = 28v?? Vrms = 44/sqrt(3)?
For the square part...Vrms and Vave both = 11v?!

So how do I get a final result?

Any help would be appreciated.

 

[gneill]

For the sinusoidal signal, express the signal as a function. Then apply the definition of RMS to that function (hint: integrate the square of the function over one period, $0 → 2 \pi$).

It's not clear from your description how the trapezoidal signal is supposed to look, or what its period is. Can you post a diagram?

 

[D44]

Hopefully you will be able to see the image I have attached

 

[gneill]

Hopefully you will be able to see the image I have attached

Alas, no...

 

[D44]

This should work...

 

[D44]

Ok, using an equation I have found, I get a value of 13.9Vrms for the trapezoidal waveform?

 

[gneill]

This should work...

Yes, that's better. In order to find the average and RMS values you'll need to specify the full period of the waveform, not just the portion with the pulse. What's the time from the y-axis (presumably t=0) to where the pulse begins?

 

[D44]

I'm told that Ton is 100-78 sorry

 

[gneill]

I'm told that Ton is 100-78 sorry

Sorry, I don't understand the specification. What are the units? How does "100-78" relate to your diagram?

 

[D44]

I'm told Ton = 100-78 ms. Ton = 22ms or 0.022s. The diagram is exactly what I have been given. So I'm taking it that the bit that the total time period is 100ms.

 

[D44]

Two more different values for the trapezoidal wave -

Vrms = 38.7V
Vave = 27.5V

Either sound correct?

 

[gneill]

Two more different values for the trapezoidal wave -

Vrms = 38.7V
Vave = 27.5V

Either sound correct?

I think they should be much smaller considering how short the pulse duration is compared to the period. Here's another diagram:

Note the long stretch before the pulse begins where the function value is 0V.

A way to simplify a problem like this is, for the sake of calculation, move the pulse so that it is left justified with the y-axis. Then you can represent it as a simple line segment going from 11V to 45V over time 0s to 22ms (keeping in mind that the full period is still 100ms, of course) That is,

$y(t) = 11 + \left( \frac{45 - 11}{22} \right) t$

Then the average and RMS integrations become simpler. For the average you would have something like:

$$Vav = \frac{1}{100} \int_0^{22} \left[ 11 + \left( \frac{45 - 11}{22}\right) t \right] \; dt$$

 

[D44]

So for Vave I get 6.16V?

I don't know how you knew to work it out like that. How did you get that function? I need to learn.

So, how would I go about getting the rms? I've seen stuff where they square everything and integrate from there, but why?

 

[gneill]

So for Vave I get 6.16mV?

6.16V (not mV if the given voltages are 11V and 45V)

I don't know how you knew to work it out like that. How did you get that function? I need to learn.

The function is that of a line passing through (0,11) and (22,45). y = mx + b. So b is 11, and the slope is (45 - 11)/22.

The average value is the integral of the function over its period divided by the period. In this instance the period of the entire waveform is 100 ms. The only "interesting" part is where the pulse exists, since the rest is zero. That's why you can shift the "interesting" bit over to the origin to simplify the function you write.

So, how would I go about getting the rms? I've seen stuff where they square everything and integrate from there, but why?

RMS stands for Root of the Mean of the Square. That means you take the function, square it, then find the average of that over the period, then take the square root.

 

[D44]

Excellent, thanks. So, Vrms I'm getting as 14.23V. This sound any better? Yeah, I realized I had made a mistake with the previous calculation. Vave = 6.16V.

 

[gneill]

Excellent, thanks. So, Vrms I'm getting as 14.23V. This sound any better? Yeah, I realized I had made a mistake with the previous calculation. Vave = 6.16V.

The RMS value should be just a tad smaller. But it's getting closer

You could show your calculations for checking...

 

[D44]

Ok, so I have...

〖V_rms〗^2=1/10 [∫_0^0.022▒〖(〖11〗^2+(2×11×((45-11)/0.022) 〗×t)+((45-11)/0.022×t)^2 ]

=(121+748+1156)/10

=202.5

∴V_rms=√202.5=14.23V

 

[D44]

Ahhh, think I might have found the problem...

I needed to subtract 11/10 which gives vrms^2 = 201.4 and so vrms = 14.19V?

 

[gneill]

You can leave the times in ms since the units will cancel when the average is taken over the period. That will keep the numbers cleaner. So if the function is:

$f(t) = 11 + \frac{45 - 11}{22} t = 11 + \frac{17}{11} t$

$f(t)^2 = 121 + 34 t + \frac{289}{121} t^2$

Integrating term by term:

$\int f(t)^2 = 121 t + 17 t^2 + \frac{289}{363} t^3$

and plugging in the bounds (0 → 22):

$= \frac{58102}{3} - 0 = 1.937 \times 10^4$

Divide by the period (100) in order to find the mean, and then take the square root:

$\sqrt{\frac{1.937 \times 10^4}{100}} = 13.92 V$