c4nc3r
- 2
- 0
Just to preface, this isn't something that I've been given as homework, I'm not currently enrolled in any schooling, however as a matter of personal interest I wanted to work out the solution to the problem without a guess-check-improve method. I have an idea, and it seems too obvious to be true but still.
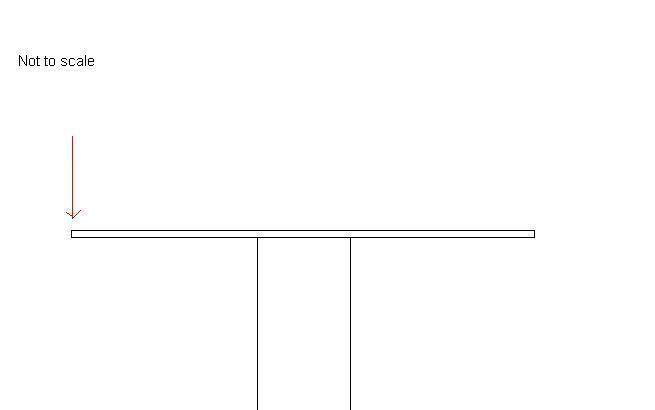
I'm building a coffee table which will consist of a sheet of glass resting on top of the block of an engine (basically, a rectangular prism on its end). I want to find out the highest weight that can be put on the very edge of the table without the glass falling off. My basic MS Paint drawing is below, with the red arrow being the weight point.
I don't yet know the weight of the glass, as I'm unsure of the size of the sheet, I'm more interested in finding an equation to use when I do know all the variables.
Not sure yet
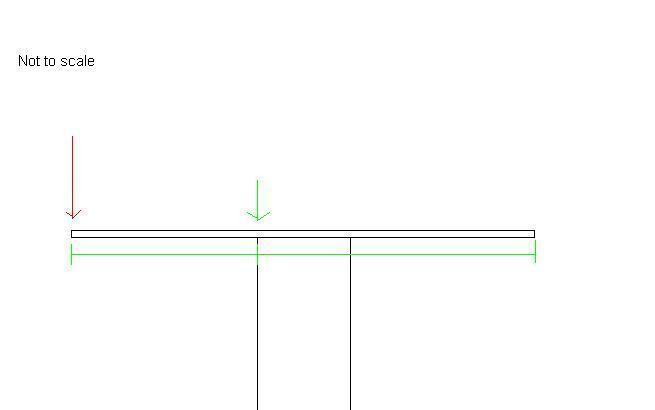
From the thinking I've been doing, it originally seemed to be simply a case of balancing the weight of the left and right hand sides, with the pivot point being the side of the block closest to the weight (see attached image)
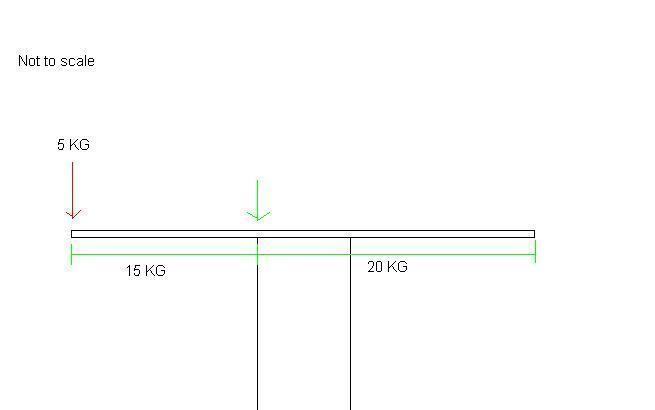
For example, the image below would be perfectly balanced and therefore wouldn't fall;
But then the more I think about it the more that seems to be too simple a breakdown, as the further from the pivot point the weight is the more force it has. So that's where I'm stumped, which is frustrating as I know I should know the answer.
I'm not sure if my explanation has made sense to anyone, if you need clarification don't hesitate to ask, and likewise if this is in the wrong place then let me know and I'll do what I can to move it.
Thanks guys
Josh
Homework Statement
I'm building a coffee table which will consist of a sheet of glass resting on top of the block of an engine (basically, a rectangular prism on its end). I want to find out the highest weight that can be put on the very edge of the table without the glass falling off. My basic MS Paint drawing is below, with the red arrow being the weight point.
I don't yet know the weight of the glass, as I'm unsure of the size of the sheet, I'm more interested in finding an equation to use when I do know all the variables.
Homework Equations
Not sure yet
The Attempt at a Solution
From the thinking I've been doing, it originally seemed to be simply a case of balancing the weight of the left and right hand sides, with the pivot point being the side of the block closest to the weight (see attached image)
For example, the image below would be perfectly balanced and therefore wouldn't fall;
But then the more I think about it the more that seems to be too simple a breakdown, as the further from the pivot point the weight is the more force it has. So that's where I'm stumped, which is frustrating as I know I should know the answer.
I'm not sure if my explanation has made sense to anyone, if you need clarification don't hesitate to ask, and likewise if this is in the wrong place then let me know and I'll do what I can to move it.
Thanks guys
Josh