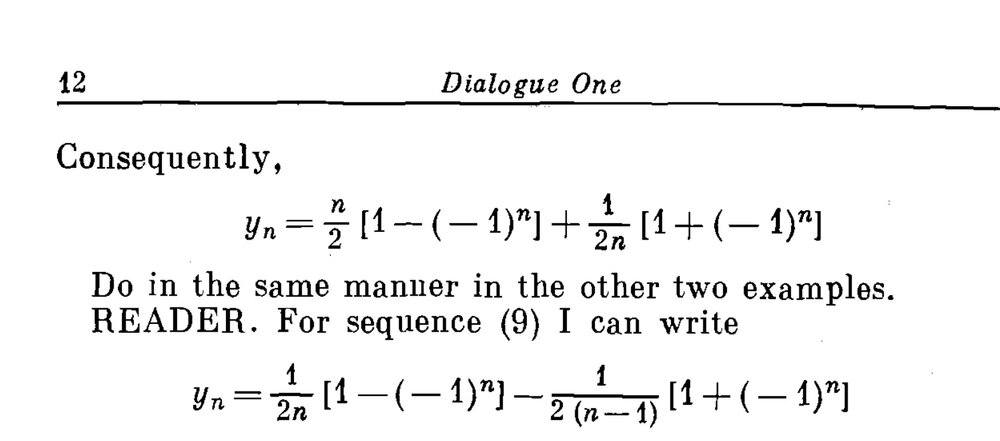Discussion Overview
The discussion revolves around a sequence presented in a Soviet calculus book, specifically examining the legitimacy of a term in the sequence that involves division by zero. Participants explore the implications of defining sequences and the conditions under which certain terms may or may not be included.
Discussion Character
- Exploratory
- Technical explanation
- Conceptual clarification
- Debate/contested
Main Points Raised
- One participant questions the legitimacy of a term in the sequence that has a coefficient of 1/0, suggesting it feels problematic.
- Another participant proposes starting the sequence at n=2 instead of n=1, arguing that omitting finitely many terms is often acceptable in analysis.
- Some participants express discomfort with the definition of an infinite numerical sequence, noting that the first term does not correspond to a natural number in the given expression.
- There is a suggestion that sequences can be defined on any infinite subset of natural numbers, with examples provided for starting points and types of numbers (odd, even, prime).
- Participants emphasize the importance of clarifying any restrictions on n when defining sequences.
- One participant notes that the pattern discussed only applies for n>1, indicating that y1 must be treated separately if absolute values are considered.
Areas of Agreement / Disagreement
Participants express varying opinions on the legitimacy of the sequence's definition and the treatment of specific terms. There is no consensus on the appropriateness of including the term with division by zero, and multiple viewpoints on how to define sequences based on different starting points remain unresolved.
Contextual Notes
Participants highlight the absence of restrictions in the book regarding the definition of the sequence, which may lead to confusion. The discussion also reflects on the implications of defining sequences based on different subsets of natural numbers.