I'll take a stab. H/W = 35/12. This is what NASA used in one of it's chambers. (70" height, 2' square base). This was a commercially supplied material.
Thinking it through:
First we need to know the reflection coefficient (gamma, but don't confuse with gamma function or you'll get string theory.

) and index of refraction. These are all frequency dependent. The index of refraction will be a complex number with the imaginary part representing the lossiness of the material at that frequency (i.e make it as big as possible for the relevant frequencies).
The incident wave will impinge at various angles primarily dependent on where the radio source is in the room. (Such echos that exist will come in at different angles). Only a few tiles will have a wave perpendicular to the wall.
This is a guess: For waves >> than W the surface might be considered a corrugated surface. I don't know the equations for corrugated surfaces, but we will want to match impedance with air (377Ω). (Corrugated surfaces have differing impedances than smooth ones.) I don't know how the impedance of the surface affects the equations compared to the assumed perfect electric conductor, but I'm sure it does. Note this applies to surface waves. I suspect some of those would develop unless suppressed.
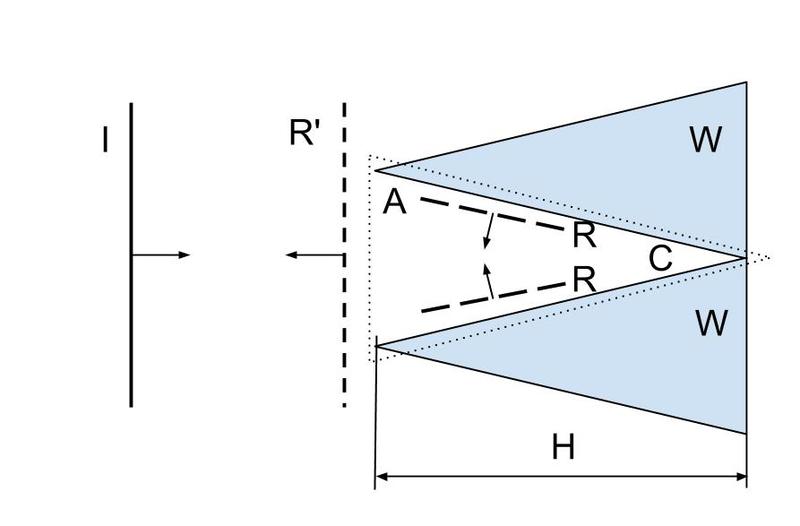
For waves << than W, we are going to want to bounce the wave off the sides of the pyramid as many times as we can. Each time some of the wave will pass into the RAM (depending on the reflection coefficient) and be attenuated while traveling through to the far wall where it will reflect again. If it's the back wall of the chamber the reflection coefficient will be different. This would argue for a shallow angle C.
For waves on the order of W, try antenna modeling software?
This isn't a great response. I hope someone can do better.