What are the accelerations of A on an incline with different scenarios?

[Matt12345]

Homework Statement

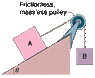
Body A weighs 110 N, and body B weighs 37 N. The coefficients of friction between A and the incline are μs = 0.56 and μk = 0.25. Angle θ is 40°. Let the positive direction of an x-axis be up the incline.

(a). Find the acceleration of A if A is initially at rest.
(... m/s^2) i

(b). Find the acceleration of A if A is moving up the incline.
(...m/s^2) i

(c). Find the acceleration of A if A is moving down the incline.
(...m/s^2) i

Homework Equations

F=ma

The Attempt at a Solution

So I am not really sure how to solve this problem at all. I have tried a few ways, none have come up with reasonable or correct answers.

I tried using...

F_T = m_A * g * sin(theta) - f_k

where f_k = mew_k * F_N
and setting F_N = g * a

I then solved for a and came out with 134 but that was wrong and didn't make sense.

I have no idea what to do next. Can anyone help me out? That would be awsome.

 

[Matt12345]

So I got part (a). which is 0. I don't know why I didn't try that before. I feel stupid. But parts (b). and (c). I am still not sure about.

 

[PhanthomJay]

So I got part (a). which is 0. I don't know why I didn't try that before. I feel stupid. But parts (b). and (c). I am still not sure about.

This problem makes no sense. Either the block A is at rest, or it moves up the plane, or moves down the plane. It can't do all three!