flydream19
- 3
- 0
1. All given variables and known data
Consider a particle of mass m subject to the infinite square well potential function (with L>0)
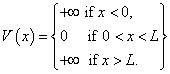
Suppose that you do not know the state function describing the system, but that you are told the expectation value of the position of the particle is given by
\left\langle x \right\rangle \left( t \right) = \frac{L}{2} + \alpha L\sin \left( {\Omega t} \right)
where α is some unknown constant less than 1/2, and Ω is some frequency greater than zero.
Questions:
Consider a particle of mass m subject to the infinite square well potential function (with L>0)
Suppose that you do not know the state function describing the system, but that you are told the expectation value of the position of the particle is given by
\left\langle x \right\rangle \left( t \right) = \frac{L}{2} + \alpha L\sin \left( {\Omega t} \right)
where α is some unknown constant less than 1/2, and Ω is some frequency greater than zero.
Homework Equations
Equations used in Quantum Mechanics
Questions:
a. There are many possible values of Ω - what are the allowed values of Ω? (That is, provide an equation for ℏΩ (h-bar*Ω) ). Explain your answer.
b. Write down the most general wave function consistent with this expectation value. Explain your answer.
b. Write down the most general wave function consistent with this expectation value. Explain your answer.