What are the domains and codomains of composed functions?

[plzen90]

Homework Statement

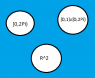
Define Function f: [0,1]x[0,2∏)→ℝ² by

f(r,θ)=

(r(2+cos5θ)cosθ)
(r(2+cos5θ)sinθ)

Let g: [0,2∏)→[0,1]x[0,2∏) be defined by

g(t)=

(1)
(t)

Compute the function δ=f°g, what are the domain and codomain of δ?

Homework Equations

The Attempt at a Solution

Replacing r with 1 and θ with t gives

(2+cos5t)cost
(2+cos5t)sint

but this doesn't seem right

Homework Statement

Homework Equations

The Attempt at a Solution

 

[Karamata]

First, did you mean $f(r,θ)=(r(2+cos5θ)cosθ,r(2+cos5θ)sinθ)$ and $g(t)=(1,t)$?

what are the domain and codomain of δ?

Look at picture (attachment), and mark the function and you will see

P.S. It seems well.

 

[plzen90]

yes, that's what I mean.

thanks for the help

I don't really understand the picture, but would the domain be the possible input of g, and the codomain the possible outputs of f?

ie domain of [0,2∏) and codomain of ℝ2 ?

 

[plzen90]

ahh I get your picture now, I think I am right with the domain and codomain?

 

[Karamata]

Yes you are.