OK, let me see if I can fill in some details without getting too technical - not that you have to put this in your essay, it's just for your understanding.
In quantum field theory, basically everything is expressed in terms of fields, functions of spatial and temporal position. Kind of like the electric field and magnetic field (but those particular fields aren't the fundamental ones in QFT). The fields basically correspond to particles.
The Higgs mechanism requires a minimum of two of these fields, which could be labeled \phi_1 and \phi_2, or they could be combined into a single complex field \phi = \phi_1 + i\phi_2. Anyway, QFT has some sort of a potential energy that's associated with these fields. It's a function of the values of the fields. If you were to graph the potential V as a function of the complex field \phi, it might look like this:
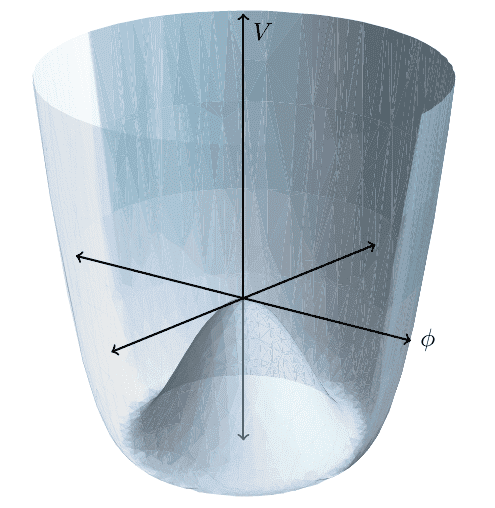
You'll notice that there is a whole ring of minimum-potential points, but the universe/particle/system/whatever you're dealing with can't be at every point on that ring simultaneously. It has to have some particular value of the field \phi - it has to be at one particular point, just as if you dropped a ball into this graph it would come to rest at one particular point on the ring. Basically, the Higgs mechanism consists of making a particular choice of coordinates to put that one particular point at the origin of the graph. You define a new complex field \eta which is a shifted version of \phi. That field \eta is the Higgs field.
Now, when you use \eta instead of \phi in the mathematics of QFT, you find that your gauge fields (the ones corresponding to the W and Z bosons) acquire a mass. For a simple example, think of this (I'm switching to real, not complex, variables now):
[(1 + A)\phi]^2 = \phi^2 + 2A\phi^2 + A^2\phi^2
In QFT, any term that contains a field variable squared times a constant (like m\phi^2) tells us the mass of that field. In the above expression, \phi has a mass of 1, but A has no mass since there's no term of the form m A^2. But when you substitute \phi \to \eta + D (this is how you shift the field), you get
[(1 + A)(\eta + D)]^2 = D^2+2 D^2 A+D^2 A^2+2 D \eta +4 D A \eta +2 D A^2 \eta +\eta ^2+2 A \eta ^2+A^2 \eta ^2
Now you see a term D^2 A^2, which means that now the particle corresponding to the field A has a mass of D^2. That's basically the gist of the Higgs mechanism.
The Higgs mechanism that gives the weak bosons mass is just a more complicated version of that. It involves four scalar fields, that could be labeled \phi_1, \phi_2, \phi_3, and \phi_4. (If you were to read papers on the subject, you'd often see them combined into two complex fields.) That's where the four degrees of freedom come from. There are also the three gauge fields for the W and Z bosons, which correspond to A in my example. I've only just started learning about this myself, so I couldn't really tell you much more than that, but hopefully that'll get you started
