Karol
- 1,380
- 22
Homework Statement
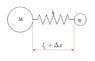
Two different size masses are attached to a pre stretched string. they are released from rest.
What are their velocities when the spring returns to initial length, just before the collision
Homework Equations
The spring constant: ##F=kx##
The Attempt at a Solution
For each mass:
##F=kx=ma\Rightarrow a=\frac{k}{m}x##
The acceleration is proportional to the displacement, i cannot integrate it because to get velocity i have to integrate acceleration with respect to time.
If i take a short interval of time Δt the acceleration is approximately constant in it:
##a=\frac{k}{m}x\cdot \delta t##
first, i don't know the time interval and secondly i will get an expression with x, what should i do with it?
##\int \frac{k}{m}x dt##