junkie_ball
- 25
- 0
Homework Statement
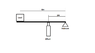
The 200Kg Crates are placed on a hydraulic lifting beam: (Diagram attached)
A. State the order of lever used here
B. Calculate the effort required to lift the load
C. Calculate mechanical advantage for this system
D. Calculate the velocity ratio for this system. If the work put in is 3000J.Calculate the useful energy output.
E. System has efficiency of 65%. Calculate the velocity ratio for this system.
Homework Equations
Effort Required = large distance x small effort = small distance x large loadMechanical advantage = load/effort
Velocity ratio = distance moved by effort/distance moved by load OR
Velocity ratio = Mechanical Advantage/Efficiency
Efficiency = output/input
Efficiency = mechanical advantage/velocity ratio
The Attempt at a Solution
A. Third Order as the effort lies between to the fulcrum and load
B. Force Effort (Fe) x Distance Effort (De) = Force Load (Fl) x Distance Load (Dl)
Fe = (Fl x Dl)/De
Fe = (200 x 6)/1
Fe = 1200N
C. Mechanical Advantage (Ma) = Load / Effort
Ma = 200/1200
Ma = 0.16 Recurring
D. This is where i have become slightly confused do i assume the system is 100% efficient for this part of the question? In which case i could use the following to calculate the valocity ratio
Velocity ratio (Vr) = Mechanical Advantage (Ma) /Efficiency (E)
Vr = 0.16/100
Vr = 0.01666 (THIS SEEMS INCORRECT TO ME)
As such the equation Velocity ratio = distance moved by effort/distance moved by load would be the one to use. The problem is i have not been given the distances moved. I know i need to take the work put in somehow to get my answer but not sure how to use this. Could someone please point me in the right direction?
E. I will calculate this once I've solved for part D