- #1
- 12,277
- 3,471
Mod note: This thread on the reactive centrifugal force was split from [thread=667584]this thread[/thread] on the (fictitious) centrifugal force.
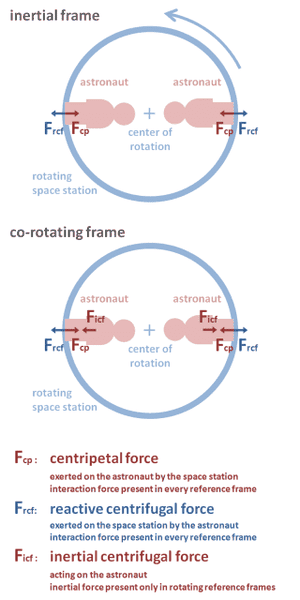
It is really not that confusing if you make clear which reference frame you consider.
sophiecentaur said:Using the term 'Centrifugal Force' when I was at school was verboten.
It is really not that confusing if you make clear which reference frame you consider.
Last edited by a moderator: