Chestermiller said:
Can you please say in words what you are trying to determine in each of these cases. I, for one, am unable to make sense out of it.
@Chestermiller, of course. Sorry I was trying to be clear but succinct. Here is an explanation in words and some of my thoughts.
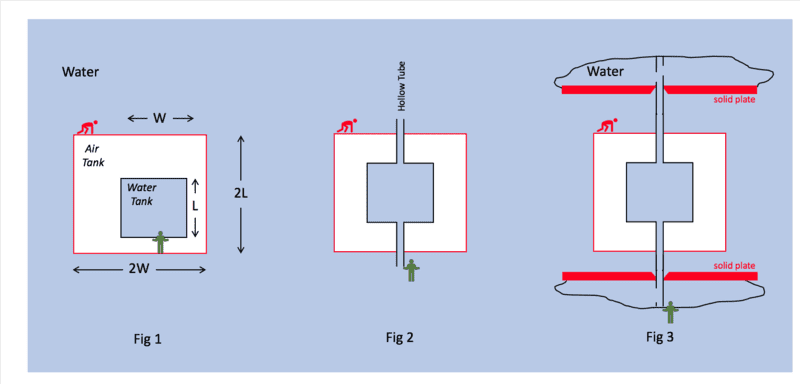
Figure 1:
I basically assert that the net force upwards (denoted by the red person pushing in the opposite direction) is due to the buoyancy upwards minus the weight downwards. I calculate this using one of two ways to arrive at the same result:
(i) by using the
total volume displaced -
including the volume of contained water - to calculate upthrust and then subtracting the
total weight -
also including the weight of the water or equivalently,
(ii) by using the volume
excluding water volume and the weight
excluding the weight of water to arrive at a net force upwards of 3LWρ
Airg - M
AirTankg - m
WaterTankg in both cases.
I then try to make the point that any internal forces (
e.g., weightless green person inside lifting the water tank) has no effect on the net forces of the entire model as all internal forces cancel one another. I do not have a question here, I am simply setting up the problem ...but feel free to comment.
Figure 2:
In this scenario, I open the water tank to the outside water pressure using two thin hollow tubes of negligible volume and weight. I assume that this tank can move relative to the Air Tank with no frictional forces (sorry, that is not clear in my original post).
This creates a scenario where, in my opinion, the force required to lift the water tank (assuming the Air Tank is held stationary) is different from
Fig 1 since the green person (regardless of whether he sits inside the air tank as in
Fig 1 or else stands outside as depicted in
Fig 2) has to lift only the weight of the tank
material (but not the weight of the
water it contains).
This question - in my opinion - also has a straightforward answer similar to the equations I show and similar to what
@sophiecentaur confirmed. I use the analogue of pushing a straw upwards through water where a single water molecule in the middle of the straw remains immobile (ignoring laminar flow and friction) as the straw moves up.
Figure 3:
This figure takes it a step further and this is where it gets interesting for me. I am asking what happens if you isolate the outside water shown in
Fig 2 with two flexible, water-filled bags as shown. My curiosity really lies in this scenario because I think the physics is identical to
Fig 2 but I would like to hear from others.
For instance, when the red person pushes the contraption up towards the bottom red solid plate, how does a water molecule in the bottom water-filled bag flow if I am not lifting the water? Does a molecule of water at the centre of the tank "theoretically" stay in place with the tank moving relative to it? Or does the red person have to bear the weight of the entire model including the contained water as in
Fig 1?