What Force Pulls m1 to the Right in a Rope-Connected System?

[floater]

First off, this isn't a homework question, its a variation on a problem I have in one of my books. I've drawn a diagram below

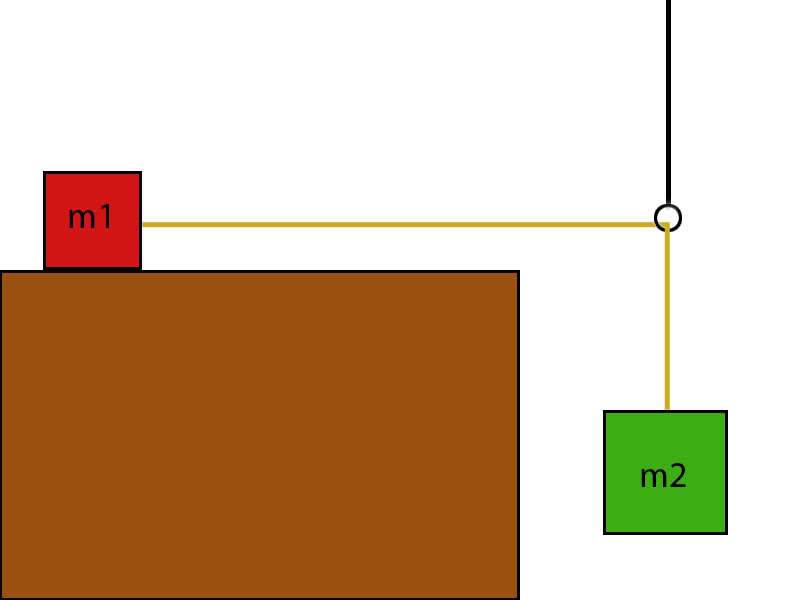
In the diagram, there are to objects of mass m1 and m2, which are connected by some rope, which is fed through that eyelet on the rod, which is perpendicular to the ceiling. I am wondering what the force is pulling m1 to the right? From my understanding, there is a force acting downwards on the rod with the eyelet, which is from the weight of m2. Now I know that this force will cause m1 to slide to the right, when it overcomes the force of friction. But I can't figure out how to explain the force pulling m1 to the right on paper.

If the rod with the eyelet was at an angle, then I could use the triangle law, but seeing as its perpendicular, there is no triangle formed. So what is indeed, pulling m1 to the right?

 

[zgozvrm]

M2 is pulling downward on the rod due to gravity. At the same time, M1 is pulling "leftward" on the rod due to friction.

 

[floater]

But what is pulling m1 to the right? I know its m2 causing tension on the rope pulling m1, but how do you show/calculate that?

 

[Redbelly98]

The rope tension pulls m1 to the right. Does that answer your question?

Also, the force exerted by the rod need not be along the direction of the rod. That is only true for things like ropes or strings.

 

[floater]

I guess what I am trying to ask is.

(ignoring friction on the eyelet)

- Does all the force pulling m2 down, ie gravity, go into pulling m1 to the right?
- Is the same force pulling m1 to the right, also acting on pulling the rod with the eyelet down? ie is the force pulling m1 to the right equal to the force pulling down on the eyelet?

 

[zgozvrm]

- Does all the force pulling m2 down, ie gravity, go into pulling m1 to the right?

Of course it does! If you removed m2 from the rope, would m1 still be pulled to the right? (No). What causes m2 to be pulled downward? (Gravity).

is the force pulling m1 to the right equal to the force pulling down on the eyelet?

No, not necessarily. That would depend (among other things) on the weights of m1 and m2. The sum of those forces would be equal to the force pulling m2 downward. Plus, the force acting to move m1 changes. At first it is large, until the friction holding it in place is overcome. Then, less force is required to keep it moving.

 

[Redbelly98]

- Is the same force pulling m1 to the right, also acting on pulling the rod with the eyelet down? ie is the force pulling m1 to the right equal to the force pulling down on the eyelet?

I'd say it's better to think along the following lines:

• There are equal-in-magnitude (and opposite in direction) forces pulling m1 to the right and the eyelet to the left.
• There are equal-in-magnitude (and opposite in direction) forces pulling m2 up, and the eyelet down.

Note, this means the eyelet is being pulled both leftward and downward.

 

[floater]

I know my questions are sounding painfully obvious, and its easy to point out the answer from common sense, but I am trying to get a more in depth understanding into the exact way things happen. So please don't think I am not applying common sense here, I am *trying* not think in terms of common sense, I am trying to think in terms of forces.

I don't want to point out what happens becuase I know that's how it happens from seeing it from day to day. I am trying to explain it purely in terms of theory.

... If that makes any sense. :)

So, regarding the following diagram. The arrows represent forces. And from my understanding f2 and f3 must add up f1. Which means that some portion of the force f1, is pulling on the rod downwards, and the rest pulling m1 to the right.

So how would you go about working out how much force is pulling down on the black rod, and how much force is pulling m1 to the right?

So is it a case of

f2.y = f1.y
f3.x = f1.y

or

f2.y + f3.x = f1.y

so putting it into numbers. And ignoring friction. If f1.y is -50, is

f2.y = -50
f3.x = 50

or

f2.y + f3.x = -50

or something completely different?

 

[Redbelly98]

Those forces are acting on different objects. There is no need for any of them to add together, nor does it make sense to do so.

If you are trying to list all forces acting on m1, m2, and the eyelet, then you are missing quite a few of them. Here is the complete list:

Forces on m1:
* gravity, downward
* normal force, upward
* rope tension, to the right
* friction, to the left (perhaps zero in this problem?)

Forces on m2:
* gravity, downward
* rope tension, upward

Forces on eyelet:
(Note: we are neglecting friction and gravity)
* tension from lower rope, acting downward
* tension from left-hand rope, acting leftward
* force from attached rod -- has both upward and rightward components.

Hope that helps with clearing things up.

 

[floater]

Thanks for the reply.

Forces on eyelet:
(Note: we are neglecting friction and gravity)
* tension from lower rope, acting downward
* tension from left-hand rope, acting leftward
* force from attached rod -- has both upward and rightward components.

* tension from left-hand rope, acting leftward <---- Wouldnt this only occur if there was friction between m1 the surface on which its on?

Also when you talk about the tension in the rope, am I right in thinking that:-

Forces on m1:
* rope tension, to the right

Forces on eyelet:
* tension from lower rope, acting downward

would be equal forces, only in different directions?

 

[Redbelly98]

Thanks for the reply.

* tension from left-hand rope, acting leftward <---- Wouldnt this only occur if there was friction between m1 the surface on which its on?

No. Perhaps (?) it will help to include the rope, which we have left out up until now.

Forces on rope:
* m1, pulling to the left
* eyelet, pulling upward and to the right
* m2, pulling down

If the rope is considered to have negligible mass, then the net force must be zero from Newton's 2nd Law, and the above three forces all sum to zero.

Also when you talk about the tension in the rope, am I right in thinking that:-

Forces on m1:
* rope tension, to the right

Forces on eyelet:
* tension from lower rope, acting downward

would be equal forces, only in different directions?

That is correct, though as I pointed out those are not the only forces acting here. I don't know why you would select just that pair of forces. Other forces that are equal to those are:

Forces on m2: rope tension, upward
Forces on eyelet: tension from left-hand rope section, acting to the left.

 

[floater]

Forces on rope:
* m1, pulling to the left
* eyelet, pulling upward and to the right
* m2, pulling down

But if there is no friction, why would m1 be pulling on the rope to the left?

 

[Redbelly98]

But if there is no friction, why would m1 be pulling on the rope to the left?

Newton's 3rd Law . If the rope pulls on m1 to the right, then m1 must be pulling the rope to the left. Lack of friction is not relevant.