What Happens to Chain Acceleration When the Thread is Burnt?

[ritwik06]

Homework Statement

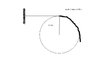
Refer to diagram for this question:
A uniform flexible chain of length 1.50 m rests on a fixed smooth sphere of radius R=\frac{2}{pi}such that one end A of the chain is at the top of the sphere while the other end B is hanging freely. Chain is held stationary by a horizontal thread PA as shown in the figure. Calculate the acceleration when the thread is burnt.

The Attempt at a Solution

I am attempting the whole solution from my side. I have even got the final answer. But I am not sure of it. Please point out errors if any.

First I calculate the length of the cirumference of the sphere to know the part of the chain which is freely hanging. I assume that mass is uniformly distributed about the chain u kg/m
So the force due to the hanging part= 0.5*u*g


consider a very small sections of the chain with length dx. The dx*u*sin\theta component is balanced by the Normal reaction.
Only the tangential force of each particle supports the motion along the boundary of the sphere. Therefore the total force supporting the motion:
[I am at present not considring the part which is hanging.]
ug\int^{\frac{\pi}{2}}_{0}dx cos \theta
dx=r* d\theta [I have doubt in this step, is it right?]
\frac{2ug}{\pi}\int^{\frac{\pi}{2}}_{0}d\theta cos \theta
=\frac{2ug}{\pi}

Net force=\frac{2ug}{\pi}+\frac{ug}{2}
Net acceleration=Net Force/Mass of Chain
a=\frac{g(4+\pi)}{3\pi}

Is this process correct?

 

[badphysicist]

You're close, but there are a few problems. It might help you to start a little farther back. Start with g\int cos\theta dm. This is really the force on the part of the chain that is being around the sphere.. if you integrate correctly. You can also apply this formula to the part hanging down, but without the cos. dm is a little piece of mass of the chain. You need to get it into other terms (things that you can integrate more easily along a curve..)