pellman
- 683
- 6
Never mind. I got this one. Couldn't figure out how to delete the post though.
Attachments
-
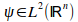 upload_2015-8-15_11-27-0.png969 bytes · Views: 559
upload_2015-8-15_11-27-0.png969 bytes · Views: 559 -
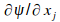 upload_2015-8-15_11-27-24.png829 bytes · Views: 564
upload_2015-8-15_11-27-24.png829 bytes · Views: 564 -
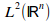 upload_2015-8-15_11-28-24.png743 bytes · Views: 562
upload_2015-8-15_11-28-24.png743 bytes · Views: 562 -
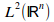 upload_2015-8-15_11-30-2.png743 bytes · Views: 542
upload_2015-8-15_11-30-2.png743 bytes · Views: 542 -
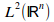 upload_2015-8-15_11-30-25.png743 bytes · Views: 558
upload_2015-8-15_11-30-25.png743 bytes · Views: 558 -
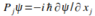 upload_2015-8-15_11-30-51.png1.1 KB · Views: 554
upload_2015-8-15_11-30-51.png1.1 KB · Views: 554
Last edited: