FrankJ777
- 140
- 6
- Homework Statement
- Take the curl in the shperical coordinate system.
- Relevant Equations
- Same as below.
This is from my E&M textbook.
I'm doing a problem where I need to take the Curl in spherical coordinates but I'm getting the wrong answer.
I tried applying the matrix, but it doesn't seem like it make sense with the expansion that they show in the textbook (screenshot below).
If I apply the matrix formula I end up with an extra sinθ that don't get if I use the formula in the expansion.
It looks to me like in the aφ component there should be a 1/sinθ factor outside the brackets?
I don't see what is happening in the aφ compentent that is making the 1/sinθ factor next to the matrix disapear when we get to the aφ component.
Am I missing something.
Thanks
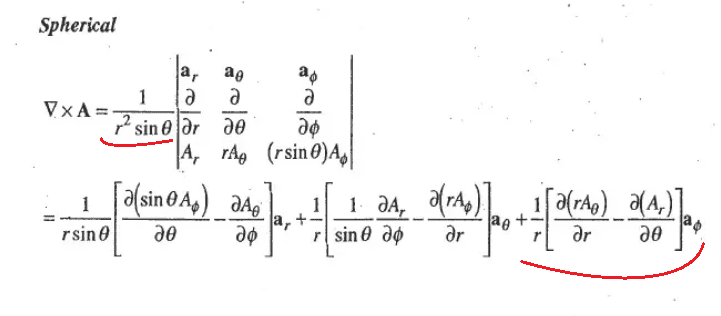
I'm doing a problem where I need to take the Curl in spherical coordinates but I'm getting the wrong answer.
I tried applying the matrix, but it doesn't seem like it make sense with the expansion that they show in the textbook (screenshot below).
If I apply the matrix formula I end up with an extra sinθ that don't get if I use the formula in the expansion.
It looks to me like in the aφ component there should be a 1/sinθ factor outside the brackets?
I don't see what is happening in the aφ compentent that is making the 1/sinθ factor next to the matrix disapear when we get to the aφ component.
Am I missing something.
Thanks