ewnair
- 3
- 0
Homework Statement
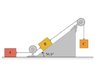
3 blocks A B C are connected by strings as in attached image. The block C is descending with constant velocity. I've worked out the tension in string A B to be 7.31N. The coefficient of kinetic friction between each block and the surface is 0.36 and block a b weighs 20.3N each. I've also calculated the weight of C to be 25.3N. The last part of the question asked for the acceleration of block C if the rope between A B is cut.
Homework Equations
Link to figure
http://b.imagehost.org/view/0603/YF-05-56.jpg
The Attempt at a Solution
I figured that if the rope was cut, the resultant force would be = t in A B which is 7.31N, working out to an equation 7.31 = (25.3/9.80) * acceleration. However the answer is wrong. The question did not provide a numerical value for g so i was wondering if i shouldn't have used 9.80. Any help would be much appreciated thanks.
Attachments
Last edited by a moderator: