SherBear
- 81
- 0
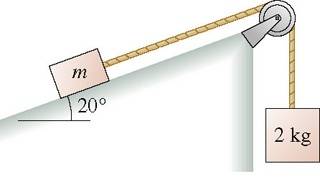
Figure shows a block of mass resting on a slope. The block has coefficients of friction and with the surface. It is connected via a massless string over a massless, frictionless pulley to a hanging block of mass 2.0 kg.
i got this first one: What is the minimum mass that will stick and not slip?
1.83 kg
Correct
But can't get the second part:
If this minimum mass is nudged ever so slightly, it will start being pulled up the incline. What acceleration will it have?
Thank you! :)
i got this first one: What is the minimum mass that will stick and not slip?
1.83 kg
Correct
But can't get the second part:
If this minimum mass is nudged ever so slightly, it will start being pulled up the incline. What acceleration will it have?
Thank you! :)