What is the acceleration of the ring on a vertical rod with a spring?

[nil1996]

Homework Statement

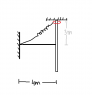
A ring is moving on a vertical rod attached to a spring. Find the velocity of the ring when spring becomes horizontal. The spring is ideal with spring constant 400N/m. Mass of ring is 10kg. Natural length of spring is 4m. Initially the ring is at rest as shown in figure.(attachment)

Homework Equations

The Attempt at a Solution

I want to solve the problem using Newtons laws and not by conservation of energy method. I have no idea on where should I start. I have made the following equation:

Fcosθ + mg = ma ...where F is the force by the spring
... θ is the angle between spring and rod
... a is the acceleration of the ring

 

[haruspex]

Next you need some geometry to relate theta to the length of the spring, and an equation relating the length of the spring to F.

 

[nil1996]

thanks for the reply Haruspex
From hooks law:
F=k*x ...where x is the length of spring.

from geometry:

cosθ=h/x

so x=h/cosθ

so F=k*h/cosθ

 

[haruspex]

thanks for the reply Haruspex
From hooks law:
F=k*x ...where x is the length of spring.

No, that would be where x is the extension of the spring.

from geometry:

cosθ=h/x

so x=h/cosθ

so F=k*h/cosθ

This way is going to get messy because h and x are both variable. Let the horizontal distance be D (=4m) and write the height and spring extension in terms of D and theta.

 

[nil1996]

No, that would be where x is the extension of the spring.

This way is going to get messy because h and x are both variable. Let the horizontal distance be D (=4m) and write the height and spring extension in terms of D and theta.

So i should write it as:

F=k(D/sinθ -3) ... D =horizontal distance

so putting this value in first equation:

ma=Fcosθ + mg

ma=k(D/sinθ-3)cosθ + mg

dv/dt = k/m(D/sinθ-3)cosθ + g

$\frac{dv}{dt}$=$\frac{k}{m}$($\frac{D}{sinθ}$-3)+g

 

[haruspex]

So i should write it as:

F=k(D/sinθ -3) ... D =horizontal distance

Not 3. The relaxed length is also D.

so putting this value in first equation:

ma=Fcosθ + mg

ma=k(D/sinθ-3)cosθ + mg

dv/dt = k/m(D/sinθ-3)cosθ + g

$\frac{dv}{dt}$=$\frac{k}{m}$($\frac{D}{sinθ}$-3)+g

You dropped the cos.

 

[nil1996]

Not 3. The relaxed length is also D.

You dropped the cos.

o,made silly mistakes.


$\frac{dv}{dt}$=$\frac{k}{m}$($\frac{D}{sinθ}$-D)cosθ + g

now what to do after this?Should we consider a small change in θ and integrate it over the "θ" range to find the velocity??

 

[haruspex]

o,made silly mistakes.


$\frac{dv}{dt}$=$\frac{k}{m}$($\frac{D}{sinθ}$-D)cosθ + g

now what to do after this?Should we consider a small change in θ and integrate it over the "θ" range to find the velocity??

You need to express the vertical height as a function of theta, and thereby express dv/dt in terms of theta.

 

[nil1996]

You need to express the vertical height as a function of theta, and thereby express dv/dt in terms of theta.

sorry but i am not getting what you saying?Can you please explain a little.