What is the area of intersection between two adjacent spherical caps?

[morjo]

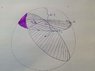
Ok, so a cube and a sphere are both centered at origo. The cube has side lengths L. I need to know the surface area of the part of the sphere that is inside the cube, for all possible r. There will be three different equations, one for 0 < r < L/2, when the entire sphere is inside the cube, one for L/2 < r < L/\sqrt(2), when six spherical caps of the sphere stick out of the cube sides , and one for L/\sqrt(2) < r < L\sqrt(3) / 2, when only the corners of the cube is visible. I have figured out the two first, but not the last.

Any help would be greatly appreciated!

 

[phinds]

You need to show some work on your own before we know where you are stuck and how to help.

 

[morjo]

OK. The reason I did not show my work is because i believe there must be a much simpler way. But her it is.

If I am not mistaking, the area X of the sphere INSIDE the cube is the total area A of the sphere, minus the area C of the six spherical caps, plus the area of the overlaps E between the caps near each of the 12 edges (because it has been subtracted twice). So X = A - 6C + 12E.

I have found A and C:
A = 4\pi R^2
C = 2\pi R h = 2 \pi R (R-L/2)

Now I only need E, the intersection / overlap between two adjacent spherical caps. In the attached drawing, the colored area is HALF of E. E has been divided in the middle by the arc of a great circle. Finding the colored area have proved more difficult than I expected, though.