c.teixeira
- 39
- 0
Hi there.
At first I tought of posting this thread on the homework category, but this is a conceptual doubt rather than anything else.
While revisiting Heat Transfer I stumbled upon a simple problem, that yet got me thinking.
It is as follows:
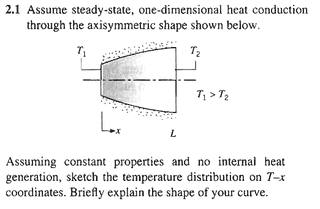
Before anything else, let me show you how they solve the problem:

Now, altough I understand and agree with their simple solution, I later tried to apply the heat equation to this problem:
\frac{\partial(κ\frac{\partial T}{\partial x})}{\partial x} + \frac{\partial(κ\frac{\partialτ}{\partial y})}{\partial y} + \frac{\partial(κ\frac{\partial T}{\partial z})}{\partial z} + \dot{q} = \rhoc_{p}\frac{\partial T}{\partial t}
Assuming constant properties, no internal heat generation, one-dimensional steady-state heat conduction:
\frac{\partial(κ\frac{\partial T}{\partial x})}{\partial x} = 0 \Leftrightarrow κ\frac{\partial^{2}T} {\partial x^{2}} = 0\Rightarrow T(x) = C_{1}x + C_{2} thus the temperature varies linearly with x.
Comparing this with the solution presented in the image, we see that they are different. Indeed, the solution may take values far apart from the linear solution, depending on the variation of A(x). Rest assured, if A = A(x), then certainly A_{x}\frac{\partial T}{\partial x} \neq Constant, as \frac{\partial T}{\partial x} = C_{1}.
But the most surprinsing is the following:
If we calculate the expression for the heat transfer rate using the linear solution:
q_{x} = -kA(x)\frac{\partial T}{\partial x} \Leftrightarrow q_{x} = -kA(x)C_{1}, and so the heat trasfer rate varies with x through A(x). And this violates the assumption that there is no sink and/or steady state condition.
Now, both the solution presented in the image, and the heat equation ( which I directly applied to this problem) are based on the conservation of energy, so clearly I am missing something. Why are this solutions so unlike if the laws, boundary bonditions and assumptions( namely steady-state, one-dimensional) are the same?
My guess is that this is explained in the following manner:
This two solutions are aproximations to a problem that is not 1 dimensional, but two dimensional. Therefore, they don't need to be equal.
What is your opinion or the matter? If my explanation is suitable, then what is the best approximation and why?
Thank you in advance,
c.teixeira
At first I tought of posting this thread on the homework category, but this is a conceptual doubt rather than anything else.
While revisiting Heat Transfer I stumbled upon a simple problem, that yet got me thinking.
It is as follows:
Before anything else, let me show you how they solve the problem:
Now, altough I understand and agree with their simple solution, I later tried to apply the heat equation to this problem:
\frac{\partial(κ\frac{\partial T}{\partial x})}{\partial x} + \frac{\partial(κ\frac{\partialτ}{\partial y})}{\partial y} + \frac{\partial(κ\frac{\partial T}{\partial z})}{\partial z} + \dot{q} = \rhoc_{p}\frac{\partial T}{\partial t}
Assuming constant properties, no internal heat generation, one-dimensional steady-state heat conduction:
\frac{\partial(κ\frac{\partial T}{\partial x})}{\partial x} = 0 \Leftrightarrow κ\frac{\partial^{2}T} {\partial x^{2}} = 0\Rightarrow T(x) = C_{1}x + C_{2} thus the temperature varies linearly with x.
Comparing this with the solution presented in the image, we see that they are different. Indeed, the solution may take values far apart from the linear solution, depending on the variation of A(x). Rest assured, if A = A(x), then certainly A_{x}\frac{\partial T}{\partial x} \neq Constant, as \frac{\partial T}{\partial x} = C_{1}.
But the most surprinsing is the following:
If we calculate the expression for the heat transfer rate using the linear solution:
q_{x} = -kA(x)\frac{\partial T}{\partial x} \Leftrightarrow q_{x} = -kA(x)C_{1}, and so the heat trasfer rate varies with x through A(x). And this violates the assumption that there is no sink and/or steady state condition.
Now, both the solution presented in the image, and the heat equation ( which I directly applied to this problem) are based on the conservation of energy, so clearly I am missing something. Why are this solutions so unlike if the laws, boundary bonditions and assumptions( namely steady-state, one-dimensional) are the same?
My guess is that this is explained in the following manner:
This two solutions are aproximations to a problem that is not 1 dimensional, but two dimensional. Therefore, they don't need to be equal.
What is your opinion or the matter? If my explanation is suitable, then what is the best approximation and why?
Thank you in advance,
c.teixeira