What is the circumference of a circle with a diameter of 1.2 meters?

  • Thread starter Thread starter Samad
  • Start date Start date
AI Thread Summary
The circumference of a circle with a diameter of 1.2 meters is calculated as approximately 3.77 meters using the formula πd. In the context of a cylinder rolling down a slope, the distance mass B is lifted is determined to be 10 meters. This total distance accounts for both the cylinder's rotation and the distance it travels down the hill. The discussion highlights the relationship between the cylinder's movement and the lifting of mass B. Overall, the calculations and concepts presented clarify the mechanics involved in the scenario.
Samad
Messages
4
Reaction score
0
Cylinder A in following figure rolls 5m down the slope. What distance is mass B lifted?
( Ans. SB= 10 m )

pulley.jpg


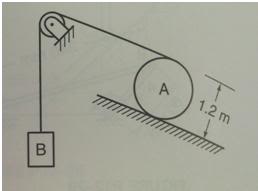
circumference of circle = πd = (3.14)(1.2) = 3.77

Not sure what to do next. I tried Pythagoras theorem, although it's probably not needed.

Please help.
 
Physics news on Phys.org
So the rope winds around the cylinder while the cylinder is moving down the hill. Suppose the rope doesn't wind around the cylinder. By how much would B be lifted? By how much does the cylinder rotate after it rolls 5 m downhill? Add the two distances together and you get 10 m.
 
Thanks man. It makes perfect sense to me now.
 

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Calculating Theoretical Reaction Force of Ball Traveling in Semi-Circle
Replies
43
Views
4K
Rotating cylinder rolling without slipping in a B field
Replies
9
Views
2K
What Is the Stopping Distance of a Mobile Machine Pushed at 1.2 m/s?
Replies
12
Views
2K
How to find distance when a ball rolls slope with angle?
Replies
1
Views
1K
Inclined plane translational velocity
Replies
5
Views
2K
Water level rise in a tank, continuous flow in, high exit
Replies
11
Views
3K
Motion of a Cylinder: Angular Velocity & Horizontal Distance
Replies
18
Views
2K
This formula is applicable for a point charge distribution.
Replies
1
Views
2K
Find magnetic field at point on Circumference
Replies
2
Views
3K
Egg tossing crime -- From what location was the egg thrown?
Replies
14
Views
3K

Hot Threads

Recent Insights

Back
Top