e4physics
- 6
- 0
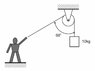
The person in the system above has a mass of 60 kg. If the system is in equilibrium, what is the coefficient of friction between the person and the ground, to two decimal places?
I need help on this question , I have done some work on it which is given below:
Converted masses into weights/forces:
for weight of man : 60*98.1 = 588.6 N
for weight of the hanging mass = 10 * 98.1 = 98.1 N
I have done the tension in the string , the man is pulling the weight.
T* COS60° = 98.1N
T = 98.1N/COS60°
T = 196.2 N
IF THE SYSTEM IS IN EQUILIBRIUM SUM OF THE FORCES SHOULD BE ZERO.
I HAVE ALSO FOUND THE OTHER COMPONENT OF T WHICH I THINK WILL BE EQUAL AND OPPOSITE THE FRICTIONAL FORCE. ITS GIVEN AS
Ty = 196.2* sin 60° = 169.9144 N
My understanding is that i need to use F = μ * W
But i am not sure about what will be W
Could someone explain this question and guide me if i have done this right.
I need help on this question , I have done some work on it which is given below:
Converted masses into weights/forces:
for weight of man : 60*98.1 = 588.6 N
for weight of the hanging mass = 10 * 98.1 = 98.1 N
I have done the tension in the string , the man is pulling the weight.
T* COS60° = 98.1N
T = 98.1N/COS60°
T = 196.2 N
IF THE SYSTEM IS IN EQUILIBRIUM SUM OF THE FORCES SHOULD BE ZERO.
I HAVE ALSO FOUND THE OTHER COMPONENT OF T WHICH I THINK WILL BE EQUAL AND OPPOSITE THE FRICTIONAL FORCE. ITS GIVEN AS
Ty = 196.2* sin 60° = 169.9144 N
My understanding is that i need to use F = μ * W
But i am not sure about what will be W
Could someone explain this question and guide me if i have done this right.