MJNZ1
- 6
- 3
- Homework Statement
- What is the acceleration due to gravity?
- Relevant Equations
- Formula 1 F = (4pi^2*m*r)/(T^2)
Formula 2 g exp. = (4pi^2*m*r)/(M*T^2) or g = (4pi^2*m*r)/(M*T) ?
Hi,
This is my first post, I hope I have done it right.
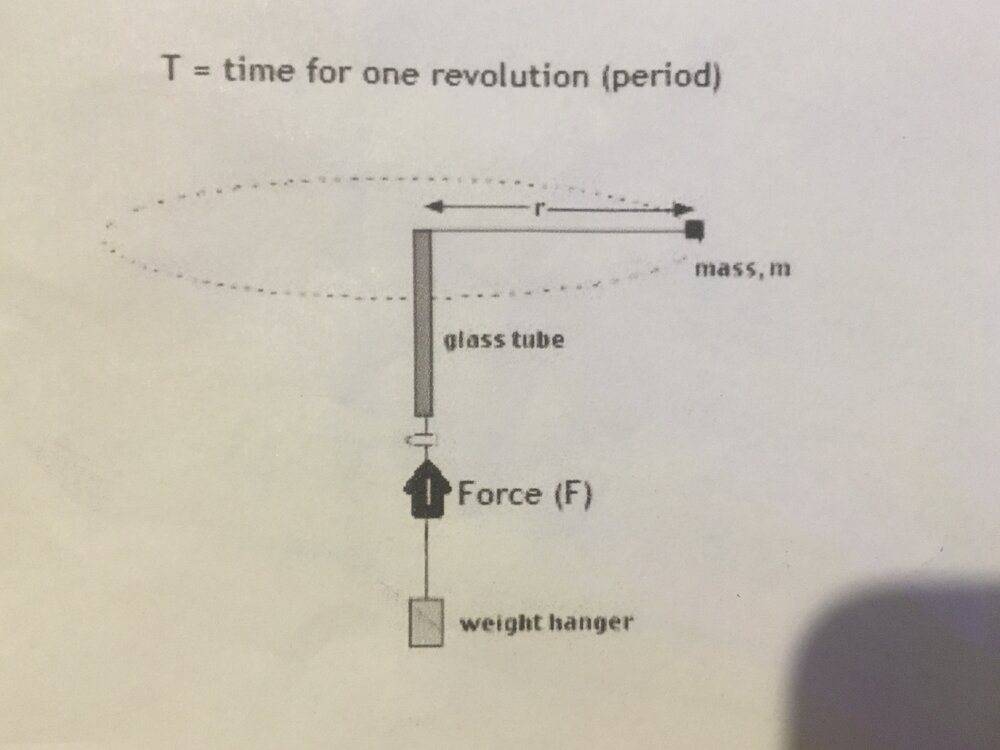
The top mass is represented as m and the weight hanger M.The image below is my attempt with the first formula 2. I have done it in grams because when I did it in kg's it was not anywhere near 9.81ms^-2...I know it is wrong :)
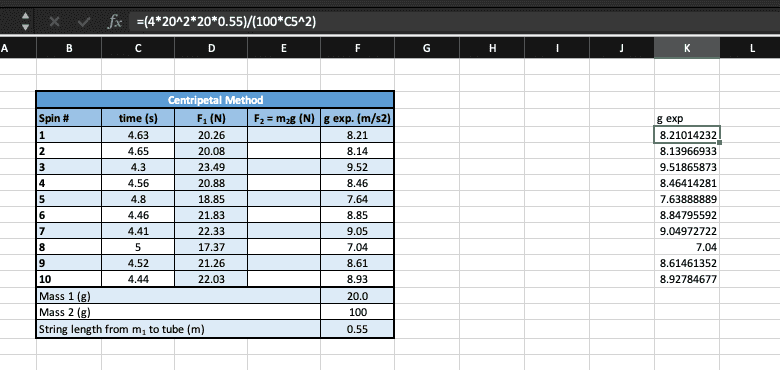
g exp. = (4pi^2*m*r)/(M*T^2) ...in kg's: (4pi^2*0.02*0.55)/(0.1*4.63^2) = 0.938ms-^2
When the teacher was asked by another student for further help understanding, the second formula 2 was given.
This is my attempt at solving for gravity from the example below in kg's: (4pi^2*0.02*.55)/(0.1*4.63) = 0.938ms^-2
g = (4pi^2*m*r)/(M*T)
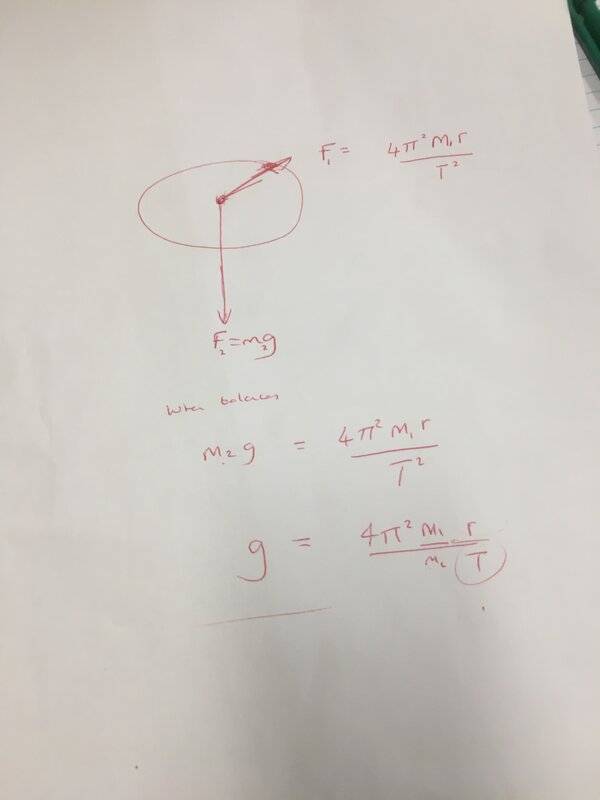
This is my first post, I hope I have done it right.
The top mass is represented as m and the weight hanger M.The image below is my attempt with the first formula 2. I have done it in grams because when I did it in kg's it was not anywhere near 9.81ms^-2...I know it is wrong :)
g exp. = (4pi^2*m*r)/(M*T^2) ...in kg's: (4pi^2*0.02*0.55)/(0.1*4.63^2) = 0.938ms-^2
When the teacher was asked by another student for further help understanding, the second formula 2 was given.
This is my attempt at solving for gravity from the example below in kg's: (4pi^2*0.02*.55)/(0.1*4.63) = 0.938ms^-2
g = (4pi^2*m*r)/(M*T)
Attachments
Last edited by a moderator:
