What is the correct way to solve for weight on two pulleys?

[Addez123]

Homework Statement

A weight starts from rest, what is its velocity after falling 0.82m? Use energy considerations.

Relevant Equations

M = 4.5 kg
R = 8.5 cm
Ip = 3 * 10^-3 kg m2
rp = 5 cm
m = 0.6 kg

I've done this exercise twice now, the answer is 1.4m/s but I get 1.64m/s. It's too far off to be rounding error.

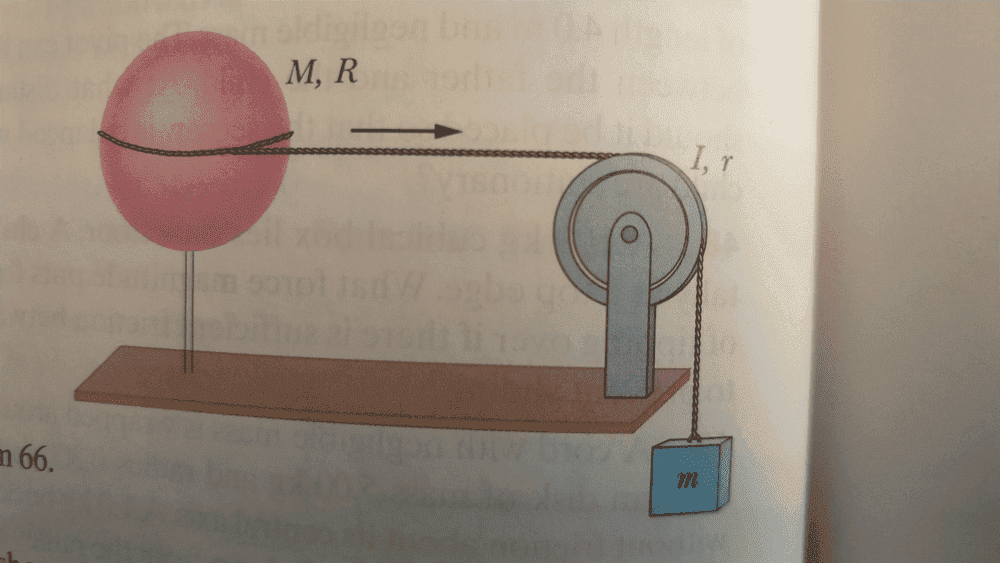
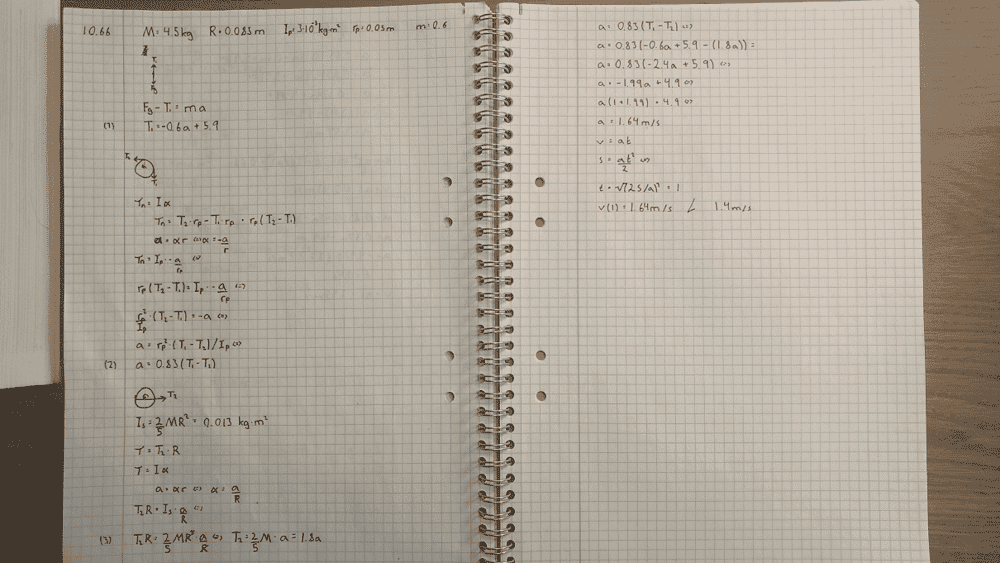
1. I don't use energy consideration, because I don't have a clue how that would work.
2. I still need to know what's wrong with my current way of solving this.

Any help is appriciated :)

 

[BvU]

Well, for 1. you make an energy balance: gravity does work (how much, you can calculate) that gets converted into kinetic energy: two things rotate and the mass takes the remainder. Much quicker than solving the equation of motion.

For 2. I need a day to decipher what the complete exercise problem statement may have been and to sleuth through your work. Getting it legibly on my screen is already daunting !
Tip: don't fill in numbers until you have worked it out completely in symbols.

 

[kuruman]

Also, is the round spherical object a solid sphere or a shell? I am asking because the figure (it was originally black & white) brought back memories from more than 50 years ago when I worked on this problem out of the first edition of Halliday and Resnick. Back then the sphere was a shell and I think one was supposed to find its angular speed, but I am not sure about that.

 

[haruspex]

Also, is the round spherical object a solid sphere or a shell? I am asking because the figure (it was originally black & white) brought back memories from more than 50 years ago when I worked on this problem out of the first edition of Halliday and Resnick. Back then the sphere was a shell and I think one was supposed to find its angular speed, but I am not sure about that.

Taking it to be a shell doesn't seem to make enough difference. I get 1.6m/s for that.
To get 1.4m/s I have to make the sphere's radius of inertia almost R.

 

[Delta2]

Doing the same calculations as you, I get 1.419m/s with the only difference that I take the moment of inertia of the sphere to be $\frac{2}{3}MR^2$ that is to be a hollow sphere.

 

[haruspex]

Doing the same calculations as you, I get 1.419m/s with the only difference that I take the moment of inertia of the sphere to be $\frac{2}{3}MR^2$ that is to be a hollow sphere.

Then I must have made an arithmetic error. Or two.

 

[Delta2]

Taking it to be a shell doesn't seem to make enough difference. I get 1.6m/s for that.
To get 1.4m/s I have to make the sphere's radius of inertia almost R.

Then I must have made an arithmetic error. Or two.

I followed the OP's approach and just replace the moment of inertia of the sphere with $\frac{2}{3}MR^2$ which leads to acceleration of about 1.22m/sec^2 and time of fall of about 1.15sec.

Did you do it with the energy approach?

 

[Addez123]

Delta2 solved it!
It was a spherical 'shell', I completely missed that part.

 

[Delta2]

Well to be honest , it was @kuruman idea that the sphere might be a spherical shell or hollow sphere, I just did the calculations to confirm it.

 

[BvU]

Delta2 solved it!
It was a spherical 'shell', I completely missed that part.

Another argument for posting the full literal problem statement: if you'd done that you probably wouldn't even have needed to post anaymore !

 

[brotherbobby]

May I just make a comment to the author of the question (Addez123) about posting our attempts in a form that is more readable. A picture taken off your attempt in a notebook is difficult for many to read. Bear in mind, this is not light reading! One has to go through your working in detail to make sense of what you have done and where you have gone wrong. This forum has a considerably advanced technique of writing equations (see LatexHelp). It would mean more time needed to post a problem but it also helps the people who are going to help you with the problem in question.

There are also excellent drawing softwares (like Inkscape, https://inkscape.org/) that help us draw images as well as a textbook. Not only can we take pride in the posting being entirely ours, we can avoid potential troubles like copyright should the matter arise.