googly_eyes
- 3
- 1
Hi, it's probably a frequent question, but I can't seem to wrap my hear around. I'm trying to understand how I reach that value, not just how to get the value.
I'm designing a vehicle with 4 wheels. It'll climb a surface with a slope theta (in degrees).
This is the FBD that I've come up with of a wheel. Following my analysis, the torque M that the motor needs to provide is simply Fr*R, where Fr is the friction force.
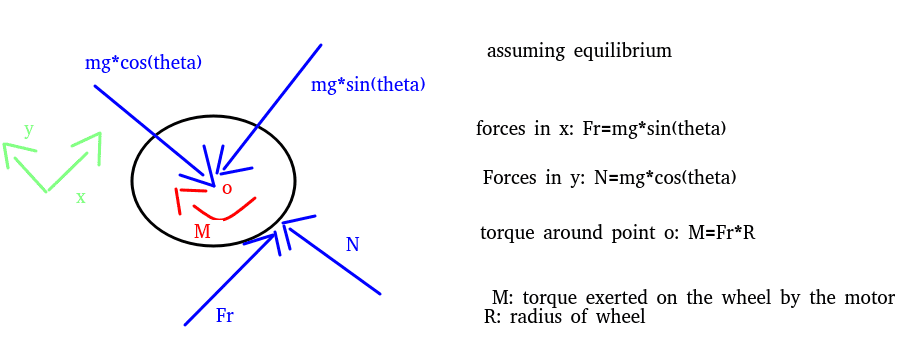
However, I've seen docs on the internet (page 35/60) that instead considers that the required torque includes an extra force (let's forget about the acceleration and wind force), which is mg*sin(theta)*R. This completely changes the torque analysis, and I don't know why it's like that (not explanation/analysis is given, just that). And I've seen the same equation on other places, including this extra member to the equation force. But alas, I'm clueless as to why it's like that. If you could please enlighten me, an explanation/FBD, whatever fits you, to explain this to me.
Many thanks
I'm designing a vehicle with 4 wheels. It'll climb a surface with a slope theta (in degrees).
This is the FBD that I've come up with of a wheel. Following my analysis, the torque M that the motor needs to provide is simply Fr*R, where Fr is the friction force.
However, I've seen docs on the internet (page 35/60) that instead considers that the required torque includes an extra force (let's forget about the acceleration and wind force), which is mg*sin(theta)*R. This completely changes the torque analysis, and I don't know why it's like that (not explanation/analysis is given, just that). And I've seen the same equation on other places, including this extra member to the equation force. But alas, I'm clueless as to why it's like that. If you could please enlighten me, an explanation/FBD, whatever fits you, to explain this to me.
Many thanks