poioip
- 10
- 0
related equations and formulas
http://en.wikipedia.org/wiki/Belt_problem#Pulley_problem
image
http://upload.wikimedia.org/wikipedia/en/0/07/Straight_Belt_pully_diagram.GIF
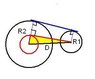
so, i need to know the equation for finding the length of the tangent.
please read https://www.physicsforums.com/showpost.php?p=3682037&postcount=5
http://en.wikipedia.org/wiki/Belt_problem#Pulley_problem
image
http://upload.wikimedia.org/wikipedia/en/0/07/Straight_Belt_pully_diagram.GIF
so, i need to know the equation for finding the length of the tangent.
please read https://www.physicsforums.com/showpost.php?p=3682037&postcount=5
Attachments
Last edited: