What is the Efficiency of a Heat Engine?

[TFM]

Homework Statement

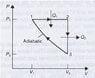
A hypothetical engine, with an ideal gas as the working substance, operates on the cycle shown in Figure 1. Show that the efficiency of this engine is

$$e = 1 - \frac{1}{\gamma}\left(\frac{1 - \frac{p_3}{p_1}}{1 - \frac{v_3}{v_1}}\right)$$

Where $$\gamma = \frac{c_p}{c_v}$$

Homework Equations

Efficiency = Benefit/Cost

Benefit = Work out

Cost = Heat in

PV = nRt

$$\Delta U = Q_{hot} - Q_{cold} - Work$$

Work = pdv

The Attempt at a Solution

The Graph is attached, but basically it has a Adiabatic curve, which at the bottom goes up vertically, then left horizontally, back to make a cycle.

So far I have:

E = Work/Cost

Work = pdv

Cost = Q

$$w = pdv$$

Since p is not constant, use ideal law,

$$w = \frac{nRt}{v}dv$$

thus

$$w = \frac{nRt}{v}dv$$

$$w = nRt [ln(v)]^{v_1}_{v_2}$$

I also have:

$$e = 1 - \frac{Q_{cold}}{Q_{hot}}$$,

from

$$\Delta U = Q_{hot} - Q_{cold} - Work$$

Which is cylci and this delta u = 0.

I am going the ruight way about this problem?

Many thanks,

TFM

 

[Redbelly98]

Efficiency = Benefit/Cost

Benefit = Work out

Cost = Heat in

PV = nRt

ΔU = Q_hot - Q_cold - Work

That's a good start. By calculating "Work out" and "Heat in", you'll be able to figure out the efficiency.

There's a problem with

$$w = nRt [ln(v)]^{v_1}_{v_2}$$

Note that T is not constant along path 31, so it must be treated as a function of V in doing the integral. Better yet forget T, keep things in terms of P. How are P and V related for an adiabatic process? (Hint: it involves γ)

 

[TFM]

Well, that would be:

$$PV^{\gamma} = Constant$$

Would you rearrange for p, and insert into:

work = pdv

 

[Redbelly98]

Yes. And another hint:

"the constant" = P₁ V₁^γ or P₃ V₃^γ (Choose either one)
​

 

[TFM]

Well, wouldn't it be:

$$p_1v_1 = p_3v_3$$

?

 

[Redbelly98]

No. That would be true for an isothermal process, since

PV = nRT = constant only if T=constant​

But this is an adiabatic process. It's not isothermal, so T changes.

 

[TFM]

I see, so I should rearrange like so,

$$pv^{\gamma} = C$$

$$p = \frac{C}{v^{\gamma}}$$

insert c

$$p = \frac{C}{v^{\gamma}}$$

insert into work:

$$Work = \frac{C}{v^{\gamma}}dv$$

Integrate:


$$Work = C\int v^{-\gamma}}dv$$


$$Work = C\left[ \frac{\gamma + 1}{v^{\gamma + 1}} \right]^{limits}$$


So does this look right?

 

[Redbelly98]

Integrate:

$$Work = C\int v^{-\gamma}}dv$$

Looks good up to here.

$$Work = C\left[ \frac{\gamma + 1}{v^{\gamma + 1}} \right]^{limits}$$

So does this look right?

Mmm, no, try that integral again.

What's ∫x^adx ?

 

[TFM]

Okay, the integral of x^a is (x^a+1) / (a + 1)

so if we say a = -gamma, x= v

$$\left[ \frac{v^{-\gamma} + 1}}{-\gamma + 1} \right]$$

$$C\left[ \frac{1}{(-\gamma + 1)v^{-\gamma + 1}} \right]$$

$$C = p_1V_1^{\gamma}$$

$$p_1V_1\left[ \frac{1}{(-\gamma + 1)v^{-\gamma + 1}} \right]$$

Does this look okay now?

 

[Redbelly98]

Uh, the algebra looks rather messy here. Can you double-check it and clean things up?

 

[TFM]

Hmm, can't see why they thing split in two. So:

{I'll use f for gamma, because gamma doesn't seem clear in latex}

$$C\int{v^{-f}}dv$$

$$C\left[\frac{v^{-f + 1}}{-f + 1}\right]$$

$$C\left[\frac{1}{v^{f + 1}(-f + 1)}\right]$$

$$C = pv^f$$

$$\left[\frac{pv^f}{v^{f + 1}(-f + 1)}\right]^{limit}_{limit}$$

Does this look okay?

 

[Redbelly98]

Two things:

1. in the denominator, the exponent should be f-1, not f+1

2. in the numerator, let's call those p1 and v1^f, since they are constants.

Otherwise it looks good.

 

[TFM]

okay so:

$$\left[\frac{p_1v_1^f}{v^{f - 1}(f - 1)}\right]^{limit}_{limit}$$

Better?

 

[womfalcs3]

The contents inside the parentheses were correct before. You just had to change the exponent.

 

[TFM]

So:

$$\left[\frac{p_1v_1^f}{v^{f - 1}(f + 1)}\right]^{limit}_{limit}$$

Is this better?

 

[Redbelly98]

Compare that with post #11, and my comments in post #12. Does it look like you made only the changes I said, or did you change something else too? (Hint: I wouldn't ask that question if what you wrote were correct.)

As a side note, this problem involves a lot of algebraic manipulation. And there is more of that to come. You will have to be very careful with the algebra if you are going to get this one.

I'm willing to help with reasoning things out, etc., but when symbols mysteriously change, or +/- signs keep appearing/disappearing for no reason, it gets very tedious for anybody assisting you.

Please, please try to be careful with the algebra. Double check things yourself, please don't keep relying on us to catch these numerous little errors.

 

[TFM]

Okay from P11:

$$\left[\frac{pv^f}{v^{f + 1}(-f + 1)}\right]^{limit}_{limit}$$

So,

1. in the denominator, the exponent should be f-1, not f+1

$$\left[\frac{pv^f}{v^{f - 1}(-f + 1)}\right]^{limit}_{limit}$$

2. in the numerator, let's call those p1 and v1^f, since they are constants.

$$\left[\frac{p_1v_1^f}{v^{f - 1}(-f + 1)}\right]^{limit}_{limit}$$

Better?

 

[Redbelly98]

Yes, good.

 

[TFM]

Okay so:

$$Work = \left[\frac{p_1v_1^f}{v^{f - 1}(-f + 1)}\right]^{limit}_{limit}$$

So I need to put this back into:

$$\Delta U = Q_{hot} - Q_{cold} - Work$$

$$\Delta U = Q_{hot} - Q_{cold} - \left[\frac{p_1v_1^f}{v^{f - 1}(-f + 1)}\right]^{limit}_{limit}$$

Now for the cycle $$\Delta U = 0$$

$$0 = Q_{hot} - Q_{cold} - \left[\frac{p_1v_1^f}{v^{f - 1}(-f + 1)}\right]^{limit}_{limit}$$

Thus

$$\left[\frac{p_1v_1^f}{v^{f - 1}(-f + 1)}\right]^{limit}_{limit} = Q_{hot} - Q_{cold}$$

Is this okay?

 

[Redbelly98]

Let's come back to that expression later. In the interest of organizing our thoughts, I suggest making a table showing W and Q for each of the three paths:

Work:
W31 = ?
W12 = ?
W23 = ?

Heat:
Q31 = ?
Q12 = ?
Q23 = ?

Once you fill in that table it should be easier to figure out the total Work, and the Heat Input, and from there figure out the efficiency.

We'll come back to the W31 expression we've been working on for the last 7-or-so posts, but first:
On which paths, if any, is W or Q equal to 0? Fill in those parts of the chart first, and we'll go from there.

 

[TFM]

Okay so
The work will be equal to 0 when dv = 0. this is the vertical straight line, which is path 23

For adiabatic, the heat that enters or leaves the system is 0, so path 13 is 0

For path 12, the work is the area under the curve so is thus (V3 - V1)*(P1)

Work:
W31 = ?
W12 = (V3 - V1)*(P1)
W23 = 0

Heat:
Q31 = 0
Q12 = ?
Q23 = ?

 

[Redbelly98]

Good, we've got all the easy parts and now we have to figure out the rest.

Let's get back to calculating W31:

$$\left[\frac{p_1v_1^f}{v^{f - 1}(-f + 1)}\right]^{limit}_{limit}$$

That's right so far. Next put in the limits on that integral and work out what W31 is.

 

[TFM]

Okay so would the limits be v3 and v 1, thus:

$$\left[\frac{p_1v_1^f}{v^{f - 1}(-f + 1)}\right]^{v_3}_{v_1}$$


$$\left[\frac{p_1v_1^f}{v_3^{f - 1}(-f + 1)}\right] - \left[\frac{p_1v_1^f}{v_1^{f - 1}(-f + 1)}\right]$$

 

[Redbelly98]

Those are the right limits, but in the wrong order. To see why, note that path 31 starts at "3" and ends at "1". So the limits are

$$\left[ \text{...} \right] ^{v1}_{v3}$$

EDIT: including figure from 1st post:

 

[TFM]

Okay, so:

$$\left[\frac{p_1v_1^f}{v_1^{f - 1}(-f + 1)}\right] - \left[\frac{p_1v_1^f}{v_3^{f - 1}(-f + 1)}\right]$$

Okay changed it. So now

Work:
W31 = $$\left[\frac{p_1v_1^f}{v_1^{f - 1}(-f + 1)}\right] - \left[\frac{p_1v_1^f}{v_3^{f - 1}(-f + 1)}\right]$$
W12 = (V3 - V1)*(P1)
W23 = 0

Heat:
Q31 = 0
Q12 = ?
Q23 = ?

 

[Redbelly98]

Looking good.

Just a side note: those p₁ v₁^f terms could just as easily be p₃ v₃^f, since that is a constant quantity along path 31. This might come in handy later, when you have to manipulate expressions to get things to look like the given answer from post #1.

What's left now are Q12 and Q23.

Q23 (the heat out) isn't really necessary for calculating efficiency, since that is really Qc here and doesn't enter into the efficiency calculation.

So we just need Q12 (the heat in, or energy cost). There are a few ways one might do this:

1. Use Q = ∫ T dS along path 12
2. Use Q = ΔU + W along path 12
3. Use ΔU = 0 = (Q12+Q23+Q31) - (W12+W23+W31) around the entire cycle

The key is to pick which one is the easiest way to arrive at the answer.

I'm going to be away from the computer for several hours, until at least 6 pm (Eastern USA time zone). See how far you can get, then I can check back later.

Once you have Q12, you'll need to calculate the final answer:

Efficiency = (W12+W23+W31) / Q12

and that will involve playing with the algebra to get it in the form given in the problem statement,

$$e = 1 - \frac{1}{f}\left(\frac{1 - \frac{p_3}{p_1}}{1 - \frac{v_1}{v_3}}\right)$$

where "f" is really γ, and I have fixed a typo (v1/v3 instead of v3/v1).

Good luck!

 

[TFM]

Okay, so I have chosen method 2,

Q = U + W along path 12

so

W = (V3 - V1)P1

$$\Delta U = C_V \Delta T$$ (P const.)

Since Ideal gas, use ideal gas law,

$$T = \frac{PV}{nR}$$

Thus:

$$T_1 = \frac{p_1v_1}{nR}$$

$$T_2 = \frac{p_1v_3}{nR}$$

So:

$$\Delta T = T_f - T_i = T_2 - T_1 = \frac{p_1v_3}{nR} - \frac{p_1v_1}{nR}$$

and thus:

$$\Delta U = C_V (\frac{p_1v_3}{nR} - \frac{p_1v_1}{nR})$$thus:

$$Q_{12} = (C_V (\frac{p_1v_3}{nR} - \frac{p_1v_1}{nR}) + (V_3 - V_1)P_1$$

Now efficiency,

$$e = \frac{W_{12} + W_{23} + W{31}}{Q_{12}}$$

$$e = \frac{\left[\frac{p_1v_1^f}{v_1^{f - 1}(-f + 1)}\right] - \left[\frac{p_1v_1^f}{v_3^{f - 1}(-f + 1)}\right] + (v_3 - v_1)p_1 + 0}{(C_V (\frac{p_1v_3}{nR} - \frac{p_1v_1}{nR}) + (V_3 - V_1)P_1}$$$$e = \frac{\left[\frac{p_1v_1^f}{v_1^{f - 1}(-f + 1)}\right] - \left[\frac{p_1v_1^f}{v_3^{f - 1}(-f + 1)}\right] + (v_3 - v_1)p_1}{(C_V (\frac{p_1v_3}{nR} - \frac{p_1v_1}{nR}) + (V_3 - V_1)P_1}$$

I am assuming there is a way to simplify this...

I will keep looking, but I am sure I can get the 1 at the neginning from the last part of the fraction, and the 1/gamma isclose, as I have 1/Cv, and gamma is just CP/Cv,

But how can I get rid of the nR's?

 

[Redbelly98]

Good, that answer is a correct expression. And yes, it must be simplified to get the asked-for expression.

It's all algebra from this point onward.

Some helpful facts:

• Anything you know that relates Cv, Cp, gamma, and nR to one another
• p1 v1^f = p3 v3^f (because path 31 is adiabatic)

Like I said, it's just playing around with the algebra at this point.

Good luck!

 

[TFM]

Okay, so:

$$\gamma = f = \frac{C_p}{C_v}$$

$$C_p - C_v = nR$$

So:

$$e = \frac{\left[\frac{p_1v_1^f}{v_1^{f - 1}(-f + 1)}\right] - \left[\frac{p_1v_1^f}{v_3^{f - 1}(-f + 1)}\right] + (v_3 - v_1)p_1}{(C_V (\frac{p_1v_3}{nR} - \frac{p_1v_1}{nR}) + (V_3 - V_1)P_1}$$

$$e = \frac{\left[\frac{p_1v_1^f}{v_1^{f - 1}(-f + 1)}\right] - \left[\frac{p_1v_1^f}{v_3^{f - 1}(-f + 1)}\right] + (v_3 - v_1)p_1}{(C_V (\frac{p_1v_3}{C_p - C_v} - \frac{p_1v_1}{C_p - C_v}) + (V_3 - V_1)P_1}$$

Now the equation has a 1/\gamma, so would this be on the right path?

$${C_v} \frac{C_p}{f}$$

$$e = \frac{\left[\frac{p_1v_1^f}{v_1^{f - 1}(-f + 1)}\right] - \left[\frac{p_1v_1^f}{v_3^{f - 1}(-f + 1)}\right] + (v_3 - v_1)p_1}{(\frac{C_p}{f} (\frac{p_1v_3}{C_p - C_v} - \frac{p_1v_1}{C_p - C_v}) + (V_3 - V_1)P_1}$$

and since p1v1 ^f = v3p3^f

$$e = \frac{\frac{p_1v_1^f}{v_1^{f - 1}(-f + 1)} - \frac{p_3v_3^f}{v_3^{f - 1}(-f + 1)} + (v_3 - v_1)p_1}{(\frac{C_p}{f} (\frac{p_1v_3}{C_p - C_v} - \frac{p_1v_1}{C_p - C_v}) + (V_3 - V_1)P_1}$$


Does this look okay?

 

[Andrew Mason]

Those are the right limits, but in the wrong order. To see why, note that path 31 starts at "3" and ends at "1". So the limits are

$$\left[ \text{...} \right] ^{v1}_{v3}$$

EDIT: including figure from 1st post:

There is a simple way to do this. Apply the first law. There is no change in U in one cycle. So the work is simply Qh-Qc = Q₁₂-Q₂₃. You just have to work out the temperatures to determine what those heats are.

AM