jimithing
- 26
- 0
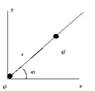
Point charges q1 and q2 are placed in space, with q1 at the origin and q2 a distance r from q1 making a 45 degree angle with the horizontal.
a) Find the force using unit vectors i and j from q1 to q2
b) " " from q2 to q1
c) If q1=q2, what is the magnitude of the force?
so far i have:
q2:
Fx = F cos (theta)
Fy = F sin (theta) - so F(1on2) = F cos(theta) i + F sin (theta) j
am I on the right track? and would F(2on1) be -F(1on2)?
a) Find the force using unit vectors i and j from q1 to q2
b) " " from q2 to q1
c) If q1=q2, what is the magnitude of the force?
so far i have:
q2:
Fx = F cos (theta)
Fy = F sin (theta) - so F(1on2) = F cos(theta) i + F sin (theta) j
am I on the right track? and would F(2on1) be -F(1on2)?
Attachments
Last edited: