antonisz
- 27
- 0
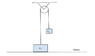
1. A 77.00 Nt object (denoted as object 1) rests on the ground. A light cord is connected to this object which runs vertically upward over a light frictionless pulley and is attached to another object denoted as object 2.
a) Calculate the force that the ground exerts on object 1 if object 2 is 30 N.
b) Calculate the force that the ground exerts on object 1 if object 2 is 60 N.
c) Calculate the force that the ground exerts on object 1 if object 2 is 90 N.
http://imgur.com/cVEQW07 http://imgur.com/cVEQW07
g (m1 - m2) / (m1) + m2 = ay I drew FBD's for both of the weights and solved for the acceleration for situation a. I then used the equation w - t = ma and solved for the tension value, I then subtracted the tension value from the original weight of object 1, and I got 33.88 N.
I feel like this is the wrong way of solving the problem because once you get to situation c, you would have a negative force which can't be possible.
a) Calculate the force that the ground exerts on object 1 if object 2 is 30 N.
b) Calculate the force that the ground exerts on object 1 if object 2 is 60 N.
c) Calculate the force that the ground exerts on object 1 if object 2 is 90 N.
http://imgur.com/cVEQW07 http://imgur.com/cVEQW07
g (m1 - m2) / (m1) + m2 = ay I drew FBD's for both of the weights and solved for the acceleration for situation a. I then used the equation w - t = ma and solved for the tension value, I then subtracted the tension value from the original weight of object 1, and I got 33.88 N.
I feel like this is the wrong way of solving the problem because once you get to situation c, you would have a negative force which can't be possible.